Derivada

En geometría, la derivada de una función en un punto representa el valor de la pendiente de la recta tangente en dicho punto. La pendiente está dada por la tangente del ángulo que forma la recta tangente a la curva (función) con el eje de las abcisas, en ese punto.

La derivada de una función mide el coeficiente de variación de dicha función. Es decir, provee una formulación matemática de la noción del coeficiente de cambio. El coeficiente de cambio indica lo rápido que crece (o decrece) una función en un punto (razón de cambio promedio) respecto del eje $x\,$ de un plano cartesiano de dos dimensiones. Por ejemplo si tomamos la velocidad de algo, su coeficiente es la aceleración, la cual mide cuánto cambia la velocidad en un tiempo dado.

La derivada de la función en el punto marcado equivale a la pendiente de la recta tangente (la gráfica de la función está dibujada en negro; la tangente a la curva está dibujada en rojo).

Conceptos y aplicaciones

El concepto de derivada es uno de los dos conceptos centrales del cálculo infinitesimal. El otro concepto es la "antiderivada" o integral; ambos están relacionados por el teorema fundamental del cálculo. A su vez, los dos conceptos centrales del cálculo están basados en el concepto de límite, el cual separa las matemáticas previas, como álgebra, trigonometría o geometría analítica, del cálculo. Quizá la derivada es el concepto más importante del cálculo infinitesimal.

La derivada es un concepto que tiene muchas aplicaciones. Se aplica en aquellos casos donde es necesario medir la rapidez con que se produce el cambio de una magnitud o situación. Es una herramienta de cálculo fundamental en los estudios de física, química y biología, o en ciencias sociales como la economía y la sociología. Por ejemplo, cuando se refiere a la gráfica de dos dimensiones de $f$, se considera la derivada como la pendiente de la recta tangente del gráfico en el punto $x$. Se puede aproximar la pendiente de esta tangente como el límite cuando la distancia entre los dos puntos que determinan una recta secante tiende a cero, es decir, se transforma la recta secante en una recta tangente. Con esta interpretación, pueden determinarse muchas propiedades geométricas de los gráficos de funciones, tales como concavidad o convexidad.

Algunas funciones no tienen derivada en todos o en alguno de sus puntos. Por ejemplo, una función no tiene derivada en los puntos en que se tiene una tangente vertical, una discontinuidad o un punto anguloso. Afortunadamente, gran cantidad de las funciones que se consideran en las aplicaciones son continuas y su gráfica es una curva suave, por lo que es susceptible de derivación.

Las funciones que son diferenciables (derivables si se habla en una sola variable), son aproximables linealmente.

Introducción geométrica a las derivadas

Es importante entender qué es una función matemática para hablar de derivadas. Una ecuación que relaciona dos variables $x\,$ e $y\,$ puede entenderse como una función, siempre y cuando a cada valor de $x\,$ le corresponda uno y solamente un valor de $y\,$. La correspondencia entre estas dos variables se puede abstraer mediante parejas $(x,y)\,$, donde $y\,$ es el valor numérico que resulta de evaluar la ecuación usando algún número $x\,$. Tales parejas se pueden interpretar como puntos geométricos en un plano cartesiano de manera que, al graficar muchos puntos, se obtiene un dibujo que representa la función.

Por ejemplo, dada la función $y={\frac {x}{x^{2}+1}}$, las parejas se obtienen dando valores arbitrarios a $x$ y calculando $y$ como se muestra en la siguiente tabla:

$y={\frac {x}{x^{2}+1}};\;y'={\frac {1-x^{2}}{(x^{2}+1)^{2}}}$

$x$ $y$ -5 -0,192... -4 -0,235... -3 -0,3 -2 -0,4 -1 -0,5 0 0,0 1 0,5 2 0,4 3 0,3 4 0,235... 5 0,192...

En esta tabla se obtienen valores para puntos $(x,y)\,$ que pueden ser graficados en un plano cartesiano con ejes $x\,$ e $y\,$. En lenguaje matemático las funciones se denotan substituyendo la variable $y\,$ por $f(x)\,$ e indicando así que $f(x)\,$ es una función de $x\,$. Es decir, indica que la variable será, en este caso, $x\,$. La función anterior tendría el aspecto

$f(x)={\frac {x}{x^{2}+1}}$

y del mismo modo, los puntos tendrían el aspecto $(x,f(x))\,$.

Se suele imaginar la derivada en un punto $x$ para la función $f(x)\,$ como la pendiente (inclinación) que existe en el punto $(x,f(x))\,$. En la gráfica de una función, la pendiente representa la rapidez con que cambia dicha función: si la pendiente es muy grande, entonces la función en este punto crece muy deprisa; si la pendiente es muy pequeña, entonces la función crece muy despacio en ese punto. En términos geométricos, esta pendiente es "la inclinación" de una línea recta que toca el punto en el que se evalúa la derivada de la función. Esta inclinación (un valor numérico) depende de la forma que tiene la función en esa zona del gráfico que la representa en el plano cartesiano.

Derivar una función no es en absoluto complicado si se sabe utilizar las reglas de derivación descubiertas por Gottfried Leibniz e Isaac Newton. Dichas reglas son fruto de un concienzudo esfuerzo puramente lógico. Se puede comparar el proceso que lleva a una regla de derivación al proceso utilizado para obtener la famosa solución que resuelve las ecuaciones de segundo grado de forma automática, y que está descrito en la mayoría de libros de texto. Se requiere un poco de práctica para aplicar correctamente la reglas de derivación sin caer en errores elementales.

Utilizando las reglas de derivación sobre una función, se obtiene otra función llamada derivada, o bien primera derivada. Si se denota por $f(x)\,$ a una función y $g(x)\,$ a la función que resulta de derivar $f(x)\,$, entonces $g(a)\,$ representa la pendiente que existe en el punto geométrico $(a,f(a))\,$. La función $g(x)\,$ representa la pendiente que posee la recta tangente a cualquier punto de la función, siendo éstos de la forma $(x,f(x))\,$. `

Condiciones de continuidad de una función

Una función continua es aquella cuya regla de correspondencia asigna incrementos pequeños en la variable dependiente a pequeños incrementos de los elementos del dominio de dicha función, es decir, $\lim _{\Delta x\to 0}\Delta y=0$, y usando la expresión $\Delta y+y=f(\Delta x+x)$, queda $\lim _{\Delta x\to 0}f(\Delta x+x)-y=0$ donde en este caso, $f(x)=y$. Ello quiere decir que $\lim _{x\to a}f_{(x)}=f_{(a)}$, y si este último límite existe significa en consecuencia por un teorema de límites (un límite existe si y sólo si los dos límites laterales existen y son iguales) que toda función $f(x)$ que cumpla con

$\lim _{x\to a+}f(x)=\lim _{x\to a-}f(x)=\lim _{x\to a}f(x)=f(a)$ es continua en el punto $a$.

Condición no recíproca

La relación no funciona a la inversa: el que una función sea continua no garantiza su derivabilidad. Es posible que los límites laterales sean equivalentes pero las derivadas laterales no; en este caso la función presenta un punto anguloso en dicho punto.

Un ejemplo puede ser la función valor absoluto (también llamada módulo) en el punto $(0,0)\,$. Dicha función es equivalente a la función partida $\left\{{\begin{matrix}x,&{\mbox{si }}x\geq 0\\-x,&{\mbox{si }}x<0\end{matrix}}\right.$

Para valores infinitamente cercanos a 0, por ambas ramas, el resultado tiende a 0. Y el resultado en el punto 0 es también 0, por lo tanto es continua. Sin embargo, las derivadas resultan $\left\{{\begin{matrix}1,&{\mbox{si }}x>0\\-1,&{\mbox{si }}x<0\end{matrix}}\right.$

Cuando $x\,$ vale 0, las derivadas laterales dan resultados diferentes. Por lo tanto, no existe derivada en el punto, a pesar de que sea continuo.

De manera informal, si el gráfico de la función tiene puntas agudas, se interrumpe o tiene saltos, no es derivable.

Definición analítica de derivada como un límite

Esquema que muestra los incrementos de la función en x y en y.

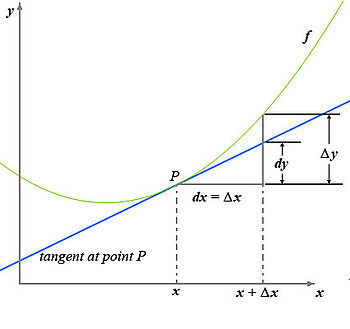
En terminología clásica, diferenciación manifiesta el coeficiente en que una cantidad "y" cambia a consecuencia de un cambio en otra cantidad "x" con la que tiene una relación funcional. Usando el símbolo "$\Delta \,$" para referirse a tal cambio, se define tal coeficiente como el límite del cociente

$\Delta y \over \Delta x$

cuando $\Delta x$ tiende (o se aproxima) a cero.

En la notación de Leibniz, se escribe la derivada de $y$ con respecto a $x$ como sigue:

$\mathrm {d} y \over \mathrm {d} x$

Esta notación depende del nombre de la función y su variable. En este caso, la función se llama "y", y la variable "x", como generalmente se designa. Esta notación sugiere la razón de dos cantidades infinitesimales.

En lenguaje matemático contemporáneo, la derivada se calcula con respecto a cantidades dependientes de una o varias variables y postula que la diferenciación es una operación matemática de carácter especial entre funciones. Se puede definir la derivada de una función en un punto del dominio en dos formas equivalentes:

1.- Definición geométrica: es la pendiente de la recta tangente a una curva en un punto específico de ella.

2.- Definición física: es la velocidad instantánea del movimiento uniformemente acelerado en un punto único del trayecto.

La definición geométrica de derivada parte del cociente de diferencias que calcula la pendiente "m" de una recta a partir de dos de sus puntos:

$m={\frac {\Delta y}{\Delta x}}={\frac {f(x+\Delta x)-f(x)}{(x+\Delta x)-x}}={\frac {f(x+\Delta x)-f(x)}{\Delta x}}$

La expresión $f(x+\Delta x)-f(x)\,$ corresponde a la variación de $f(x)\,$. Es decir: $\Delta y=f(x+\Delta x)-f(x)\,$

Esta es $\mathrm {d} y\,$, ya que $f(x)\,$ se expresa en el eje $y$. La variación en el eje $x$ corresponde a $\Delta x\,$.

Aproximación sucesiva de la recta secante a la recta tangente en x=xo

Hasta ahora se ha obtenido la pendiente de una recta secante a la curva. Si tomamos $\Delta x\,$ cada vez más pequeños, cuando sea infinitesimal (extremadamente pequeño), la diferencia entre la recta secante y la tangente será infinitesimal, pues la pendiente de la recta secante se aproxima, cada vez más, a la pendiente de la recta tangente a la curva en un punto del dominio, es decir, será el límite de la pendiente m cuando $\Delta x\,$ tiende a cero (como muestra la figura).

De este modo, queda constituida de la siguiente manera la derivada como una función:

$f'(x)=\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}=\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}$,

siempre que este límite exista, es decir, se requiere que la derivada por la izquierda y por la derecha existan y sean iguales.

La notación f ' ( x ) ("efe prima de equis") fue introducida en el siglo XVII por el matemático francés Joseph Louis Lagrange e indica que se deriva de la función original f (x).

Esta definición de derivada como límite es una de las expresiones más importantes de toda la matemática e indica analíticamente: el límite del cociente de dos diferenciales. Si se la observa con atención, se nota que se trata de un límite indeterminado de la forma 0 / 0, por lo que es muy conveniente practicar muchos límites indeterminados de ese tipo antes del cálculo de la derivada por definición.

De manera similar, considerando por simplicidad el incremento en x como h, en lugar de $\Delta x$, se define la derivada de un modo más conveniente para el cálculo como sigue:

$f'(x)=\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}=\lim _{k\rightarrow 0}{\frac {f(x)-f(x-k)}{k}}$

La primera expresión representa un acercamiento por la derecha de la pendiente de la secante a la pendiente de la tangente y en la segunda tal acercamiento es por la izquierda. Ambas proveen la regla de los cuatro pasos para el cálculo de la derivada de una función y son más sencillas de calcular que considerando la derivada como límite del cociente de dos diferenciales. Dicha regla es un cálculo algebraico por lo que se emplean técnicas apropiadas de factorización, racionalización u operaciones con fracciones, según el caso.

Al calcular la derivada por definición, el paso clave consiste en expresar el cociente diferencial de tal manera que se elimine h / h (o k / k) de manera apropiada, de modo que resulte un límite libre de la indeterminación 0 / 0.

Se puede demostrar que también puede definirse la derivada como sigue:

$f'(x)=\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x-h)}{2h}}$,

en la cual existe un acercamiento simétrico por ambos lados de la pendiente de la recta secante a la pendiente de la recta tangente y sirve de base para la derivación numérica.

Del modo más general, se define la derivada de una función como:

$f'(x)=\lim _{h,k\rightarrow 0^{+}}{\frac {f(x+h)-f(x-k)}{h+k}}$,

en la que el acercamiento es también por ambos lados y puede ser simétrico o asimétrico según sea h igual o distinta de k respectivamente.

Esta última expresión constituye la aproximación más veloz a la derivada, puesto que el acercamiento a la pendiente de la recta tangente es tanto por la derecha como por la izquierda de manera simultánea, pero es más laboriosa de calcular algebraicamente por la regla de los cuatro pasos. También puede definirse alternativamente la derivada de una función en cualquier punto de su dominio de la siguiente manera:

$f'(x)=\lim _{h\rightarrow x}{\frac {f(x)-f(h)}{x-h}}$,

la cual representa un acercamiento de la pendiente de la secante a la de la tangente ya sea por la derecha o por la izquierda según el signo de h, en la cual es posible cancelar siempre el factor " x - h " en lugar de solo h. El aspecto de este límite está relacionado más con la velocidad instantánea del movimiento uniformemente acelerado que con la pendiente de la recta tangente a una curva.

No obstante su aparente diferencia, el cálculo de la derivada por definición con cualquiera de los límites anteriormente expresados, proporciona siempre el mismo resultado. El estudiante debe utilizar el que le resulte más conveniente.

En particular, se tiene que la derivada de la función en el punto x = a (varios autores prefieren utilizar la notación "xo" en lugar de a) se define como sigue:

$f'(a)=\lim _{h\rightarrow 0}{\frac {f(a+h)-f(a)}{h}}=\lim _{x\rightarrow a}{\frac {f(x)-f(a)}{x-a}}$,

si este límite existe, de lo contrario, f '(a) no está definida. Esta última expresión coincide con la velocidad instantánea del movimiento continuo uniforme acelerado en cinemática.

Aunque podrían calcularse todas las derivadas empleando la definición de derivada como un límite, para lo cual se tendría que ser muy hábil en el cálculo de límites indeterminados de la forma 0 sobre 0 (lo cual sería muy laborioso), existen reglas bien establecidas, conocidas como teoremas para el cálculo de derivadas, las cuales permiten calcular la derivada de una función de acuerdo a su forma sin tener que calcular forzosamente el límite y hacer los cuatro pasos cada vez. Tales reglas se deducen sucesivamente de la definición de derivada y de reglas previas, como puede apreciarse en todo buen texto de cálculo infinitesimal.

El conocimiento de todas las expresiones anteriores y su significado representan el acercamiento epistémico más completo posible en torno a la definición de derivada, y con ello, al aspecto esencial del cálculo diferencial.

Notación

Existen diversas formas para nombrar a la derivada. Si f es una función, se escribe la derivada de la función $f\,$ al valor $x\,$ en varios modos:

• $f'(x)\,$ {Notación de Lagrange}

se lee "$f\,$ prima de equis"

• $\mathrm {D} _{x}f\,$ o $\partial _{x}f\,$ {Notaciones de Cauchy y Jacobi, respectivamente}

se lee "$d\,$ sub $x\,$ de $f\,$", y los símbolos D y d deben entenderse como operadores.

• ${\dot {x}}$ { Notación de Newton}

se lee "punto $x\,$" o "$x\,$ punto". Actualmente está en desuso en Matemáticas puras, sin embargo se sigue usando en áreas de la física como la mecánica, donde otras notaciones de la derivada se pueden confundir con la notación de velocidad relativa. Se usa para definir la derivada temporal de una variable.

• ${\frac {\mathrm {d} y}{\mathrm {d} x}}$, ${\frac {\mathrm {d} f}{\mathrm {d} x}}$ ó ${\frac {\mathrm {d} }{\mathrm {d} x}}f(x)$ {Notación de Leibniz}

se lee "derivada de $y\,$ ($f\,$ ó $f\,$ de $x\,$) con respecto a $x\,$". Esta notación tiene la ventaja de sugerir a la derivada de una función con respecto a otra como un cociente de diferenciales.

La notación más simple para diferenciación, en uso actual, es debida a Lagrange. Para identificar las derivadas de $f(x)\,$ en el punto $a$, se escribe:

$f^{\prime }(a)$ para la primera derivada,

$f^{\prime \prime }(a)$ para la segunda derivada,

$f^{\prime \prime \prime }(a)$ para la tercera derivada,

$f^{(n)}(a)\,$ para la enésima derivada ($n>3$). (También se pueden usar números romanos).

Para la función derivada de $f(x)\,$, se escribe $f^{\prime }(x)\,$. De modo parecido, para la segunda derivada de $f(x)\,$ se escribe $f^{\prime \prime }(x)\,$, y así sucesivamente.

La otra notación común para la diferenciación es debida a Leibniz. Para la función derivada de $f(x)\,$, se escribe:

${\frac {\mathrm {d} \left(f(x)\right)}{\mathrm {d} x}}.$

Con esta notación, se puede escribir la derivada de $f$ en el punto $a$ de dos modos diferentes:

${\frac {\mathrm {d} \left(f(x)\right)}{\mathrm {d} x}}\left.{\!\!{\frac {}{}}}\right|_{x=a}=\left({\frac {\mathrm {d} \left(f(x)\right)}{\mathrm {d} x}}\right)(a).$

Si $y=f(x)\,$, se puede escribir la derivada como

$\mathrm {d} y \over \mathrm {d} x$

Las derivadas sucesivas se expresan como

${\frac {\mathrm {d} ^{n}\left(f(x)\right)}{\mathrm {d} x^{n}}}$ o ${\frac {\mathrm {d} ^{n}y}{\mathrm {d} x^{n}}}$

para la enésima derivada de $f(x)\,$ o de $y$ respectivamente. Históricamente, esto viene del hecho que, por ejemplo, la tercera derivada es

${\frac {\mathrm {d} \left({\frac {\mathrm {d} \left({\frac {\mathrm {d} \left(f(x)\right)}{\mathrm {d} x}}\right)}{\mathrm {d} x}}\right)}{\mathrm {d} x}}$

la cual se puede escribir como

$\left({\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{3}\left(f(x)\right)={\frac {\mathrm {d} ^{3}}{\left(\mathrm {d} x\right)^{3}}}\left(f(x)\right).$

La notación de Leibniz es muy útil, por cuanto permite especificar la variable de diferenciación (en el denominador); lo cual es pertinente en caso de diferenciación parcial. También facilita recordar la regla de la cadena, porque los términos "d" parecen cancelarse simbólicamente:

${\frac {\mathrm {d} y}{\mathrm {d} x}}={\frac {\mathrm {d} y}{\mathrm {d} u}}\cdot {\frac {\mathrm {d} u}{\mathrm {d} x}}.$

En la formulación popular del cálculo mediante límites, los términos "d" no pueden cancelarse literalmente, porque por sí mismos son indefinidos; son definidos solamente cuando se usan juntos para expresar una derivada. En análisis no-estándar, no obstante, se puede ver como números infinitesimales que se cancelan.

La notación de Newton para la diferenciación respecto al tiempo, era poner un punto arriba del nombre de la función:

${\dot {x}}={\frac {\mathrm {d} x}{\mathrm {d} t}}=x^{\prime }(t)$

${\ddot {x}}=x^{\prime \prime }(t)$

y así sucesivamente.

Esta notación de Newton se usa principalmente en mecánica, normalmente para derivadas de tiempo tales comos velocidad y aceleración, y en teoría de ecuaciones diferenciales ordinarias. Usualmente solo se usa para las primeras y segundas derivadas.

Diferenciabilidad

Una función es diferenciable en un punto $x$ si su derivada existe en ese punto; una función es diferenciable en un intervalo si es diferenciable en todos los puntos del intervalo. Si una función no es continua en un punto $x$, no tiene línea tangente y, por tanto, la función no es diferenciable en ese punto; sin embargo, aunque una función sea continua en $x$, puede no ser diferenciable en dicho punto. En otras palabras, diferenciabilidad implica continuidad, pero no su recíproco.

La derivada de una función diferenciable puede ser, a su vez, diferenciable. La derivada de una primera derivada se llama derivada segunda. De un modo parecido. La derivada de una derivada segunda es la derivada tercera, y así sucesivamente. Esto también recibe el nombre de derivación sucesiva o derivadas de orden superior.

Cociente de diferencias de Newton

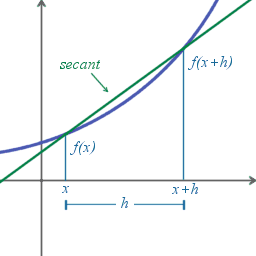
La derivada de una función $f\,$ es la pendiente geométrica de la línea tangente del gráfico de $f\,$ en $x\,$. Sin el concepto que se va a definir, no es posible encontrar directamente la pendiente de la línea tangente a una función dada, porque solamente se conoce un punto en la línea tangente: $(x,f(x))\,$. La idea es aproximar la línea tangente con múltiples líneas secantes que tienen distancias progresivamente más pequeñas entre los dos puntos que cruzan. Cuando se toma el límite de las pendientes de las líneas secantes de esta progresión, se consigue la pendiente de la línea tangente. Se define, pues, la derivada tomando el límite de la pendiente de las líneas secantes, al acercarlas a la línea tangente.

Para encontrar las pendientes de las líneas secantes próximas, se elige un número relativamente pequeño $h\,$. $h\,$ representa un cambio relativamente pequeño en $x\,$, y puede ser positivo o negativo. La pendiente de la línea que cruza los dos puntos $(x,f(x))\,$ y $(x+h,f(x+h))\,$ es

$f(x+h)-f(x) \over h$.

Archivo:Secante-calculo.svg

Inclinación de la secante de la curva y=f(x)

Esta expresión es el cociente de diferencias de Newton. La derivada de $f$ en $x$ es el límite del valor del cociente diferencial, conforme las líneas secantes se aproximan a la línea tangente:

$\displaystyle f^{\prime }(x)=\lim _{h\to 0}{f(x+h)-f(x) \over h}$.

Si la derivada de $f\,$ existe en todos los puntos $x\,$, se puede definir la derivada de $f\,$ como la función cuyo valor en cada punto $x\,$ es la derivada de $f\,$ en $x\,$.

Puesto que sustituir $h\,$ por 0 produce una división por cero, calcular directamente la derivada puede no ser intuitivo. Una técnica posible consiste en operar en el numerador, de manera que se puede cancelar la $h\,$ del denominador. Y eso es posible fácilmente en los polinomios. Pero para muchas otras funciones el resultado es incierto. Afortunadamente, hay reglas generales que facilitan diferenciar la mayoría de las funciones simples.

Sea $f\,$ una función continua, y $C\,$ su curva. Sea $x=a\,$ la abscisa de un punto regular, es decir donde $C\,$ no hace un ángulo. En el punto $A(a,f(a))\,$ de $C\,$ se puede trazar la tangente a la curva. Su coeficiente director, o sea su pendiente, es $f^{\prime }(a)$, el número derivado de $f\,$ en $a\,$.

La función $a\rightarrow f^{\prime }(a)$ es la derivada de $f\,$.

En el punto de contacto, conociendo la pendiente de la tangente, es decir $f^{\prime }(a)$, se puede saber a qué ritmo crece o decrece la función. El signo de $f^{\prime }(a)$ determina en función $f\,$ (si crece o no).

En este gráfico se ve que donde $f\,$ es creciente, las tangentes apuntan hacia arriba (mirando de izquierda a derecha), y por lo tanto $f^{\prime }\,$ es positiva, como en el punto $D\,$ ($x=d\,$), mientras que donde $f\,$ es decreciente, las tangentes apuntan hacia abajo y $f^{\prime }$ es negativa, como en el punto $B\,$ ($x=b\,$). En los puntos $A\,$ y $C\,$, que son máximo y mínimo local, la tangente es horizontal, luego $f^{\prime }(a)=0=f^{\prime }(c)$.

La función derivada se puede calcular sin dibujar la curva de $f$. En efecto, gracias a una propiedad geométrica de la tangente, se tiene la fórmula:

$f^{\prime }(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}$

Por ejemplo, sea

$f\left(x\right)=x^{2}$

entonces:

${\begin{array}{rcl}f^{\prime }(x)&=&\displaystyle \lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}\\&=&\displaystyle \lim _{h\to 0}{\frac {(x+h)^{2}-x^{2}}{h}}\\&=&\displaystyle \lim _{h\to 0}{\frac {x^{2}+2xh+h^{2}-x^{2}}{h}}\\&=&\displaystyle \lim _{h\to 0}{\frac {2xh+h^{2}}{h}}\\&=&\displaystyle \lim _{h\to 0}(2x+h)\\&=&2x\end{array}}$

Lista de derivadas de funciones elementales

$f\left(x\right)=a$	$f'\left(x\right)=0$
$f\left(x\right)=x$	$f'\left(x\right)=1$
$f\left(x\right)=ax$	$f'\left(x\right)=a$
$f\left(x\right)=ax+b$	$f'\left(x\right)=a$
$f\left(x\right)=x^{n}$	$f'\left(x\right)=nx^{n-1}$
$f\left(x\right)={\sqrt {x}}$	$f'\left(x\right)={\frac {1}{2{\sqrt {x}}}}$
$f\left(x\right)=e^{x}$	$f'\left(x\right)=e^{x}$
$f\left(x\right)=\ln(x)$	$f'\left(x\right)={\frac {1}{x}}$
$f\left(x\right)=a^{x}(a>0)$	$f'\left(x\right)=a^{x}\ln(a)$
$f\left(x\right)=\log _{b}(x)$	$f'\left(x\right)={\frac {1}{x\ln(b)}}$
$f\left(x\right)={\frac {1}{x^{n}}}=(x^{n})^{-1}=x^{-n}$	$f'\left(x\right)=-nx^{-n-1}=-nx^{-(n+1)}={\frac {-n}{x^{n+1}}}$
$f\left(x\right)=\operatorname {sen} (x)$	$f'\left(x\right)=\cos(x)$
$f\left(x\right)=\cos(x)$	$f'\left(x\right)=-\operatorname {sen} (x)$
$f\left(x\right)=\tan(x)$	$f'\left(x\right)=\sec ^{2}(x)={\frac {1}{cos^{2}(x)}}=1+\tan ^{2}(x)$
$f\left(x\right)=\csc(x)$	$f'\left(x\right)=-\csc(x)\cot(x)$
$f\left(x\right)=\sec(x)$	$f'\left(x\right)=\sec(x)\tan(x)$
$f\left(x\right)=\cot(x)$	$f'\left(x\right)=-\csc ^{2}(x)$
$f\left(x\right)=\operatorname {arcsen} (x)$	$f'\left(x\right)={\frac {1}{\sqrt {1-x^{2}}}}$
$f\left(x\right)=\arccos(x)$	$f'\left(x\right)={\frac {-1}{\sqrt {1-x^{2}}}}$
$f\left(x\right)=\arctan(x)$	$f'\left(x\right)={\frac {1}{1+x^{2}}}$
$f\left(x\right)=g(x)\pm h(x)$	$f'\left(x\right)=g'(x)\pm h'(x)$
$f\left(x\right)=g(x)\cdot h(x)$	$f'\left(x\right)=g'(x)\cdot h(x)+g(x)\cdot h'(x)$
$f'\left(x\right)={\frac {g'(x)\cdot h(x)-g(x)\cdot h'(x)}{h^{2}(x)}}$
$f\left(x\right)=k\cdot g(x)$	$f'\left(x\right)=k\cdot g'(x)$
$f\left(x\right)=g\circ h=g(h(x))$	$f'\left(x\right)=(g'\circ h)\cdot h'=g'(h(x))\cdot h'(x)$

Ejemplo

Sea $f\,$ la función $f(x)=2x^{3}-9x^{2}-24x+51\,$, definida sobre el conjunto de los números reales (denotado por $\mathbb {R} \,$). Para conocer sus variaciones se observa su derivada:

$f^{\prime }(x)=6x^{2}-18x-24$

Para encontrar el signo de $f^{\prime }(x)$, se tiene que factorizar:

${\begin{array}{rcl}f^{\prime }(x)&=&6(x^{2}-3x-4)\\&=&6(x+1)(x-4)\end{array}}$

lo anterior que se hace resolviendo una ecuación de segundo grado.

En la tabla siguiente se establece los signos de los factores (descartando el factor 6, siempre positivo), luego el signo de la derivada, y para terminar las variaciones de la función $f\,$.

El signo de la derivada primera muestra cuando crece o decrece la función.

Generalizaciones

El concepto simple de derivada de una función real de una sola variable ha sido generalizado de varias maneras:

• Cálculo de varias variables
  • Derivada direccional, extiende el concepto de derivada parcial.
  • Derivada parcial, que se aplica a funciones reales de varias variables.
• Análisis complejo:
• Función holomorfa, que extiende el concepto de derivada a cierto tipo de funciones de variables complejas
• Análisis funcional:
  • Derivada fraccional, que extiende el concepto de derivada de orden superior a orden r, r no necesita ser necesariamente un número entero como sucede en las derivadas convencionales.
  • Derivada funcional, que se aplica a funcionales cuyos argumentos son funciones de un espacio vectorial de dimensión no finita.
  • Derivada en el sentido de las distribuciones, extiende el concepto de derivada a funciones generalizadas o distribuciones, así puede definirse la derivada de una función discontinua como una distribución.
• Diferenciablidad, otra generalización posible para funciones de varias variables cuando existen derivadas continuas en todas direcciones es el de:
• Función diferenciable, que se aplica a funciones reales de varias variables que poseen derivadas parciales según cualquiera de las variables (El argumento de una función de varias variables pertenece a un espacio del tipo $\mathbb {R} ^{n}$ de dimensión n finita).
• La diferenciación en el sentido de Fréchet generaliza el concepto de función diferenciable a espacios de Banach de dimensión infinita.

Véase también

• Criterio de la derivada de mayor orden
• Pendiente de una recta
• Límite de una función
• Tabla de derivadas
• Derivación numérica
• Derivación de funciones trigonométricas
• Función matemática
• Integral