Diferencia entre revisiones de «Triángulo»
Sin resumen de edición |
m Revertidos los cambios de 83.57.75.21 (disc.) a la última edición de Tirithel |
||
| Línea 1: | Línea 1: | ||
{{otros usos|Triángulo (desambiguación)}} |
|||
[[Archivo: illustration.svg |
[[Archivo:Triangle illustration.svg|thumb|El triángulo es un polígono de tres lados]] |
||
Un |
Un '''triángulo''', geométricamente hablando, es un [[polígono]] determinado por tres [[recta]]s que se cortan dos a dos en tres [[punto]]s (que no se encuentran alineados). |
||
Los puntos de intersección de las rectas son los [[ |
Los puntos de intersección de las rectas son los [[vértice (geometría)|vértices]] y los segmentos de recta determinados son los lados del triángulo. Dos lados contiguos forman uno de los ángulos interiores del triángulo. |
||
Por lo tanto, un triángulo tiene 3 elementos: 3 |
Por lo tanto, un triángulo tiene 3 elementos: 3 ángulo interiores, 3 lados y 3 vértices. |
||
Si está contenido en una superficie [[ |
Si está contenido en una superficie [[plano (geometría)|plana]] se denomina '''triángulo''', o '''trígono''', un nombre menos común para este tipo de polígonos. Si está contenido en una superficie [[esfera|esférica]] se denomina '''[[triángulo esférico]]'''. Representado, en [[cartografía]], sobre la superficie terrestre, se llama '''triángulo geodésico'''. |
||
== Convención de escritura == |
|||
[[Archivo: |
[[Archivo:Triangle.Labels.svg|250px|thumb|Un triángulo llamado ''ABC'']] |
||
Los puntos principales de una figura geométrica, como los vértices de un polígono, |
Los puntos principales de una figura geométrica, como los vértices de un polígono, suelen ser designados por letras latinas mayúsculas: '''''A''''', ''''' B''''', '''''C''''', ...'' |
||
Un triángulo se nombra entonces como |
Un triángulo se nombra entonces como cualquier otro polígono, nombrando sucesivamente sus vértices, por ejemplo '''''ABC'''''. |
||
El orden de citación de los vértices es irrelevante, |
El orden de citación de los vértices es irrelevante, porque todos los segmentos de los que estos vértices son los extremos, son los lados del triángulo. |
||
Los lados del triángulo, |
Los lados del triángulo, son llamados, como todos los segmentos, por sus extremos: '''''AB''''', '''''BC''''' y '''''AC''''', en nuestro ejemplo. |
||
Para |
Para nombrar la ''longitud'' de un lado, por lo general se utiliza el nombre del vértice opuesto, convertido a minúscula latina: '''<math>a</math>''' para '''''BC''''', '''<math>b</math>''' para '''''AC''''', '''<math>c</math>''' para '''''AB'''''. |
||
La notación general para el ángulo entre dos |
La notación general para el ángulo entre dos segmentos '''''OP''''' y '''''OQ''''' que comparten el extremo '''''O''''' es <math>\widehat{POQ} .\,</math> |
||
También podemos |
También podemos utilizar una letra minúscula, griega lo más a menudo, coronada por un acento circunflejo (en rigor, los ángulos deben ser designados por letras mayúsculas y su medida por minúsculas, pero a menudo se utilizan los mismos nombres para los dos con el fin de simplificar la notación). En el caso de un triángulo, el ángulo entre dos lados todavía puede, por tolerancia y en ausencia de ambigüedad, ser designado por el nombre del vértice común, coronado por un acento circunflejo. En resumen, en nuestro ejemplo, podemos observar los ángulos: |
||
: |
:<math>\widehat{\alpha} = \widehat{a} = \widehat{A} = \widehat{BAC} ,\ \widehat{\beta} = \widehat{b} = \widehat{B} = \widehat{ABC} \ et\ \widehat{\gamma} = \widehat{c} = \widehat{C} = \widehat{ACB} . \,</math> |
||
<br |
<br style="clear:both" /> |
||
== Clasificación de los triángulos == |
== Clasificación de los triángulos == |
||
Los triángulos |
Los triángulos se pueden clasificar por la longitud de sus lados o por la amplitud de sus ángulos. |
||
=== Por la longitud de sus lados === |
=== Por la longitud de sus lados === |
||
| Línea 33: | Línea 33: | ||
Por la longitud de sus lados, los triángulos se clasifican en: |
Por la longitud de sus lados, los triángulos se clasifican en: |
||
*'''[[ ]]''': |
* '''[[Triángulo equilátero]]''': si sus tres lados tienen la misma longitud (los tres [[ángulo]]s internos miden 60 [[grado sexagesimal|grados]] ó <math>\pi/3\,</math> [[radián|radianes]].) |
||
*'' |
* '''Triángulo isósceles''': si tiene dos lados de la misma longitud. Los ángulos que se oponen a estos lados tienen la misma medida. |
||
*'' |
* '''Triángulo escaleno''': si todos sus lados tienen longitudes diferentes. En un triángulo escaleno no hay ángulos con la misma medida. |
||
{| align="center" |
|||
|----- |
|----- align="center" |
||
| [[Archivo: |
| [[Archivo:Triangle.Equilateral.svg|Triángulo Equilátero]] |
||
| [[Archivo: |
| [[Archivo:Triangle.Isosceles.svg|Triángulo Isósceles]] |
||
| [[Archivo: |
| [[Archivo:Triangle.Scalene.svg|Triángulo Escaleno]] |
||
|----- |
|----- align="center" |
||
| |
| Equilátero || Isósceles || Escaleno |
||
| |
|} |
||
=== Por la amplitud de sus ángulos === |
=== Por la amplitud de sus ángulos === |
||
| Línea 51: | Línea 51: | ||
Por la amplitud de sus ángulos, los triángulos se clasifican en: |
Por la amplitud de sus ángulos, los triángulos se clasifican en: |
||
*'''[[ |
* '''[[Triángulo rectángulo]]''': si tiene un ángulo interior recto (90°). A los dos lados que conforman el ángulo recto se les denomina ''catetos'' y al otro lado ''hipotenusa''. |
||
*'' |
* '''Triángulo obtusángulo''': si uno de sus ángulos es obtuso (mayor de 90°); los otros dos son agudos (menor de 90°). |
||
*'' |
* '''Triángulo acutángulo''': cuando sus tres ángulos son menores a 90°; el triángulo equilátero es un caso particular de triángulo acutángulo. |
||
{| align="center" |
|||
|----- |
|----- align="center" |
||
| [[Archivo: |
| [[Archivo:Triangle.Right.svg|Triángulo Rectángulo]] |
||
| [[Archivo: |
| [[Archivo:Triangle.Obtuse.svg|Triángulo Obtusángulo]] |
||
| [[Archivo: |
| [[Archivo:Triangle.Acute.svg|Triángulo Acutángulo]] |
||
|----- |
|----- align="center" |
||
| Rectángulo | |
| Rectángulo || Obtusángulo || Acutángulo |
||
|----- |
|----- align="center" |
||
| | |
| || colspan="2" | <math>\underbrace{\qquad \qquad \qquad \qquad \qquad \qquad}_{}</math> |
||
|----- |
|----- align="center" |
||
| | |
| || colspan="2" | Oblicuángulos |
||
| |
|} |
||
Se llama triángulo oblicuángulo |
Se llama triángulo oblicuángulo cuando ninguno de sus ángulos interiores son rectos (90°). Por ello, los triángulos obtusángulos y acutángulos son oblicuángulos. |
||
<! |
<!-- **'''Triángulo equiángulo''': suele llamarse [[Triángulo equilátero]] clasificándolo según sus lados, puesto que si sus lados son iguales, sus ángulos también lo serán, y medirán 60º. --> |
||
=== Clasificación según los lados y los ángulos === |
=== Clasificación según los lados y los ángulos === |
||
Los triángulos acutángulos |
Los triángulos acutángulos pueden ser: |
||
*'' |
* '''Triángulo acutángulo isósceles''': con todos los ángulos agudos, siendo dos iguales, y el otro distinto, este triángulo es simétrico respecto de su altura. |
||
*'' |
* '''Triángulo acutángulo escaleno''': con todos sus ángulos agudos y todos diferentes, no tiene eje de simetría. |
||
*'' |
* '''Triángulo acutángulo equilátero''': sus tres lados y sus tres ángulos son iguales; las tres alturas son ejes de simetría (dividen al triángulo en dos triángulos iguales). |
||
Los triángulos rectángulos |
Los triángulos rectángulos pueden ser: |
||
*'' |
* '''Triángulo rectángulo isósceles''': con un angulo recto y dos agudos iguales (de 45° cada uno), dos lados son iguales y el otro diferente: los lados iguales son los catetos y el diferente es la hipotenusa. Es simétrico respecto a la altura de la hipotenusa, que pasa por el ángulo recto. |
||
*'' |
* '''Triángulo rectángulo escaleno''': tiene un ángulo recto, y todos sus lados y ángulos son diferentes. |
||
Los triángulos obtusángulos |
Los triángulos obtusángulos pueden ser: |
||
*'' |
* '''Triángulo obtusángulo isósceles''': tiene un ángulo obtuso, y dos lados iguales que son los que forman el ángulo obtuso; el otro lado es mayor que éstos dos. |
||
*'' |
* '''Triángulo obtusángulo escaleno''': tiene un ángulo obtuso y todos sus lados son diferentes. |
||
<center> |
<center> |
||
{|class="wikitable" border="1" |
|||
! Triángulo |
! Triángulo |
||
| [[triángulo equilátero|equilátero]] |
|||
| [[Triángulo equilatero | equilatero]] |
|||
| [[ |
| [[triángulo isósceles|isósceles]] |
||
| [[ |
| [[triángulo escaleno|escaleno]] |
||
| |
|- |
||
| acutángulo |
|||
| Acutángulo |
|||
| [[Archivo: |
| [[Archivo:Triángulo equilátero.svg|120px]] |
||
| [[Archivo: |
| [[Archivo:Triángulo acutángulo isósceles.svg|120px]] |
||
| [[Archivo: |
| [[Archivo:Triángulo acutángulo escaleno.svg|120px]] |
||
| |
|- |
||
| rectángulo |
|||
| Rectángulo |
|||
| |
| |
||
| [[Archivo: |
| [[Archivo:Triángulo rectángulo isósceles.svg|120px]] |
||
| [[Archivo: |
| [[Archivo:Triángulo rectángulo escaleno.svg|120px]] |
||
| |
|- |
||
| obtusángulo |
|||
| Obtusángulo |
|||
| |
| |
||
| [[Archivo: |
| [[Archivo:Triángulo obtusángulo isósceles.svg|120px]] |
||
| [[Archivo: |
| [[Archivo:Triángulo obtusángulo escaleno.svg|120px]] |
||
| |
|}</center> |
||
Congruencia de triángulos |
== Congruencia de triángulos == |
||
Dos triángulos son congruentes si hay una correspondencia entre sus vértices de tal |
Dos triángulos son congruentes si hay una correspondencia entre sus vértices de tal manera que el ángulo del vértice y los lados que lo componen sean congruentes con los del otro triángulo. |
||
Postulados de congruencia |
=== Postulados de congruencia === |
||
{| class="wikitable" border="1" |
|||
! Triángulo!! Postulado |
! Triángulo !! Postulado |
||
| |
|- |
||
| [[Archivo: |
| [[Archivo:Postulado LAL.svg|100px]] |
||
| |
|| '''Postulado LAL'''<br />(Lado, Ángulo, Lado) |
||
Dos lados en un triángulo |
Dos lados en un triángulo tienen la misma longitud que dos lados en el otro triángulo, y los ángulos comprendidos entre esos lados tengan también la misma medida. |
||
| |
|- |
||
| [[Archivo: |
| [[Archivo:Postulado ALA.svg|100px]] |
||
| |
|| '''Postulado ALA'''<br />(Ángulo, Lado, Ángulo) |
||
Dos ángulos interiores y el lado comprendido entre ellos, en un triángulo, |
Dos ángulos interiores y el lado comprendido entre ellos, en un triángulo, tienen la misma medida y longitud, respectivamente con los del otro triángulo. (El lado comprendido para un par de ángulos es el lado que es común a ellos). |
||
| |
|- |
||
| [[Archivo: |
| [[Archivo:Postulado LLL.svg|100px]] |
||
| |
|| '''Postulado LLL'''<br />(Lado, Lado, Lado) |
||
Cada lado de un triángulo tiene la misma longitud que un lado del otro triángulo |
Cada lado de un triángulo tiene la misma longitud que un lado correspondiente del otro triángulo. |
||
| |
|- |
||
| |
| |
||
| |
|| '''Postulado AAL'''<br />(Ángulo, Ángulo, Lado) |
||
Dos ángulos y un lado |
Dos ángulos y un lado correspondiente no comprendido entre los ángulos, en un triángulo, tienen la misma medida y longitud, respectivamente, que las del otro triángulo. |
||
| |
|} |
||
Semejanza de triángulos |
== Semejanza de triángulos == |
||
{{AP|Triángulos semejantes}} |
|||
Dos triángulos son |
Dos triángulos son semejantes si sus ángulos tienen la misma amplitud y los lados opuestos de estos ángulos son proporcionales. |
||
*'' |
* '''Criterio aa''' (ángulo, ángulo). Si dos de sus ángulos son semejantes |
||
*'' |
* '''Criterio lal''' (lado, ángulo, lado). Si dos de sus lados son proporcionales y el ángulo comprendido entre ellos es congruente. |
||
*'' |
* '''Criterio lll''' (lado, lado, lado). Si sus tres lados son proporcionales. |
||
=== Semejanzas de triángulos rectángulos === |
=== Semejanzas de triángulos rectángulos === |
||
Dos [[ |
Dos [[triángulo rectángulo|triángulos rectángulos]] son semejantes si cumple con al menos uno de los criterios siguientes: |
||
* Si uno tiene un ángulo agudo de |
* Si uno tiene un ángulo agudo de igual amplitud que un ángulo agudo del otro. |
||
* Si uno tiene los dos catetos proporcionales con los del otro. |
* Si uno tiene los dos catetos proporcionales con los del otro. |
||
* Si uno tiene un cateto y la hipotenusa proporcionales con los del otro. |
* Si uno tiene un cateto y la hipotenusa proporcionales con los del otro. |
||
== Propiedades de los triángulos == |
== Propiedades de los triángulos == |
||
[[Archivo: |
[[Archivo:Geometrie quadrilataire.png|200px|left|thumb| Un cuadrilátero con sus diagonales]] |
||
[[Archivo: |
[[Archivo:120px-Tetrahedron-slowturn.gif|120px||thumb| Un tetraedro]] |
||
Un |
Un ''triángulo'' puede ser definido como un [[polígono]] de tres lados, o como un polígono con tres vértices. |
||
Después del [[punto]] y el [[segmento]], el triángulo es el polígono más simple. Es el único que no tiene |
Después del [[punto]] y el [[segmento]], el triángulo es el polígono más simple. Es el único que no tiene diagonal. En el espacio, tres puntos definen un triángulo (y un plano). ''Por el contrario'', si cuatro puntos de un mismo plano forman un [[cuadrilátero]], cuatro puntos que no estén en el mismo plano no definen un polígono, sino un [[tetraedro]] |
||
Por otra parte, cada polígono |
Por otra parte, cada polígono puede ser dividido en un número finito de triángulos que se forman con una [[triangulación]] del polígono. El número mínimo de triángulos necesarios para esta división es <math>n-2</math>, donde ''n'' es el número de lados del polígono. El estudio de los triángulos es fundamental para el estudio de otros polígonos, por ejemplo para la demostración del [[Teorema de Pick]]. |
||
[[Archivo: |
[[Archivo:Triangle with notations 2.svg|right]] |
||
* Los tres [[ángulo interno |
* Los tres [[ángulo interno|ángulos internos]] de un triángulo miden '''180°''' lo que equivale a π [[Radián|radianes]], en [[geometría euclidiana]].<ref>En la [[geometría no euclidiana]], como la de [[Bernhard Riemann|Riemann]] y [[Nikolai Ivanovich Lobachevsky|Lobachevsky]] la suma de los ángulos internos es diferente a 180[[grado|°]].</ref> |
||
[[Archivo: sommeangles.svg |
[[Archivo:Triangle sommeangles.svg|right|300px|thumb| La suma de los ángulos de un triángulo es 180 grados.]] |
||
Euclides había |
Euclides había demostrado este resultado en sus ''Elementos'' (proposición I-32) de la siguiente manera: trazamos la paralela a la línea (AB) que pasa por C. Siendo paralelas, esta recta y la recta (AB) forman con la recta (AC) ángulos iguales, codificados en color rojo en la figura de al lado ([[ángulos alternos-internos]]). Del mismo modo, los ángulos codificados en color azul son iguales ([[ángulos correspondientes]]). Por otro lado, la suma de los tres ángulos del vértice ''C'' es el ángulo llano. Así que la suma de las medidas del ángulo de color rojo, del ángulo verde y del azul es un ángulo de 180 ° (o π radianes). La suma de los ángulos de un triángulo es 180 °. |
||
Esta propiedad es el resultado de la geometría |
Esta propiedad es el resultado de la geometría euclidiana. No se verifica en general en la geometría no euclidiana. |
||
* La suma de las longitudes de dos de sus lados es |
* La suma de las longitudes de dos de sus lados es siempre mayor que la longitud del tercer lado. |
||
* El valor de la paralela |
* El valor de la paralela media de un triángulo (recta que une dos puntos medios de dos lados) es igual a la mitad del lado paralelo. |
||
* |
* Para cualquier triángulo se verifica el [[Teorema del seno]] que establece: «Los lados de un triángulo son proporcionales a los senos de los ángulos opuestos»: |
||
: |
:<math>\frac{a}{\operatorname{sen}(\alpha\,)} = \frac{b}{\operatorname{sen}(\beta\,)} = \frac{c}{\operatorname{sen}(\gamma\,)}</math> |
||
[[Archivo: |
[[Archivo:Pythagorean.svg|thumb|El teorema de Pitágoras gráficamente.]] |
||
* |
* Para cualquier triángulo se verifica el [[Teorema del coseno]] que demuestra que «El cuadrado de un lado es igual a la suma de los cuadrados de los otros lados menos el doble del producto de estos lados por el coseno del ángulo comprendido»: |
||
: |
:<math>a^2=b^2+c^2-2bc \cdot cos(\alpha\,)\,</math> |
||
: |
:<math>b^2=a^2+c^2-2ac \cdot \cos(\beta\,)\,</math> |
||
: |
:<math>c^2=a^2+b^2-2ab \cdot \cos(\gamma\,)\,</math> |
||
* |
* Para cualquier triángulo rectángulo, cuyos catetos miden ''a'' y ''b'', y cuya hipotenusa mida ''c'', se verifica el [[Teorema de Pitágoras]]: |
||
: |
:<math> a^2 + b^2 = c^2 \,</math> |
||
<br |
<br style="clear:both" /> |
||
== Centros del triángulo == |
|||
[[Geometría |
[[Geometría|Geométricamente]] se pueden definir varios [[Centro (Geometría)|centros]] en un triángulo: |
||
*'''[[ |
* '''[[Baricentro]]''': es el [[Punto (geometría)|punto]] que se encuentra en la [[intersección]] de las [[Mediana (Geometría)|medianas]], y equivale al [[centro de gravedad]] |
||
*'''[[ |
* '''[[Circuncentro]]''': es el [[Centro (Geometría)|centro]] de la [[circunferencia]] circunscrita, aquella que pasa por los tres [[vértice]]s del triángulo. Se encuentra en la [[intersección]] de las [[mediatriz|mediatrices]] de los [[lado]]s. Además, la circunferencia circunscrita contiene los puntos de intersección de la mediatriz de cada lado con las bisectrices que pasan por el vértice opuesto. |
||
*'''[[ |
* '''[[Incentro]]''': es el [[Centro (Geometría)|centro]] de la [[circunferencia]] inscrita, aquella que es [[tangente]] a los [[lado]]s del triángulo. Se encuentra en la [[intersección]] de las [[Bisectriz|bisectrices]] de los [[ángulo]]s. |
||
*'''[[ |
* '''[[Ortocentro]]''': es el [[Punto (geometría)|punto]] que se encuentra en la [[intersección]] de las alturas. |
||
*'''[[ |
* '''[[Exincentro]]s''': son los [[Centro (Geometría)|centros]] de las [[circunferencia]]s exinscritas, aquellas que son [[tangente]]s a los [[lado]]s del triángulo. Se encuentra en la [[intersección]] de una [[bisectriz]] interior y dos [[Bisectriz|bisectrices]] exteriores de los [[ángulo]]s. |
||
El único caso en que los cuatro primeros centros coinciden en un único punto es en un triángulo |
El único caso en que los cuatro primeros centros coinciden en un único punto es en un triángulo equilátero. |
||
== Cálculo de elementos en un triángulo == |
== Cálculo de elementos en un triángulo == |
||
Para resolver triángulos |
Para resolver triángulos utilizamos generalmente el [[Teorema de Pitágoras]] cuando son triángulos rectángulos, o los Teoremas [[Teorema del seno|del seno]] y [[Teorema del coseno|del coseno]]. |
||
== Elementos notables de un triángulo == |
== Elementos notables de un triángulo == |
||
=== |
=== Medianas y centro de gravedad === |
||
{{AP| Mediana (geometría)}} |
|||
[[Archivo: medianes.png |
[[Archivo:Triangle medianes.png|thumb|250 px|Medianas y centro de gravedad de un triángulo]] |
||
Se lama'''''''''' |
Se lama '''''mediana''''' de un triángulo cada una de las tres líneas que pasan por un vértice del triángulo y por el punto medio del lado opuesto al vértice. |
||
Cada una de las tres medianas dividen el triángulo en dos triángulos de áreas iguales. |
Cada una de las tres medianas dividen el triángulo en dos triángulos de áreas iguales. |
||
Las tres medianas de un triángulo son concurrentes. Su punto de intersección'' |
Las tres medianas de un triángulo son concurrentes. Su punto de intersección '''<math>G</math>''' es llamado '''''[[centro de gravedad]] ''''' del triángulo. |
||
<br |
<br style="clear:both" /> |
||
=== Mediatrices círculo circunscrito |
=== Mediatrices y círculo circunscrito === |
||
[[Archivo: |
[[Archivo:Triangle.Circumcenter.svg|thumb|250 px|Mediatrices y círculo circunscrito de un triángulo.]] |
||
Se llama'''''''''' |
Se llama '''''mediatriz''''' de un triángulo a cada una de las [[Mediatriz|mediatrices]] de sus lados '''<math>[AB]</math>''', '''<math>[AC]</math>''' et '''<math>[BC]</math>'''. |
||
Las tres mediatrices de un triángulo son concurrentes en un punto'' |
Las tres mediatrices de un triángulo son concurrentes en un punto '''<math> \Omega </math>''' equidistante de los tres vértices. El círculo de centro '''<math> \Omega </math>''' y radio '''<math> \Omega A</math>''' que pasa por cada uno de los tres vértices del triángulo es el '''''círculo circunscrito''''' al triángulo. |
||
Notas: |
Notas: |
||
* Un triángulo es |
* Un triángulo es obtusángulo si y sólo si las bisectrices se cortan fuera del triángulo. |
||
* Un triángulo es acutángulo si y sólo si |
* Un triángulo es acutángulo si y sólo si las bisectrices se cortan dentro del triángulo. |
||
Propiedad: |
Propiedad: |
||
*'' |
* '''<math>ABC</math>''' es un triángulo rectángulo en '''<math>A</math>''' si y sólo si el centro de su círculo circunscrito es el centro de '''<math>[BC]</math>'''. |
||
<br |
<br style="clear:both" /> |
||
=== Bisectriz círculo inscrito |
=== Bisectriz y círculo inscrito === |
||
[[Archivo: |
[[Archivo:Triangle.Incircle.svg|thumb|250 px|Bisectrices y círculo inscrito de un triángulo.]] |
||
Las'''''''''' |
Las '''''bisectrices''''' de un triángulo son las tres [[bisectriz]]es de sus ángulos internos. |
||
Las tres bisectrices de un triángulo son concurrentes en un punto'' |
Las tres bisectrices de un triángulo son concurrentes en un punto '''O'''. El '''''[[círculo inscrito]]''''' del triángulo es el único círculo tangente a los tres lados del triángulo y está totalmente incluido en el triángulo. Tiene por punto central '''O''', que es pues el '''centro del círculo inscrito''' en el triángulo. |
||
<br |
<br style="clear:both" /> |
||
Alturas y ortocentro |
=== Alturas y ortocentro === |
||
{{AP|Ortocentro}} |
|||
[[Archivo: |
[[Archivo:Triangle.Orthocenter.svg|thumb|250 px|Alturas y ortocentro de un triángulo]] |
||
Se llama'''''''''' |
Se llama '''''altura ''''' de un triángulo a cada una de las tres líneas que pasan por un vértice del triángulo y son perpendiculares a la cara opuesta al vértice. La intersección de la altura y el lado opuesto se denomina «pie» de la altura. |
||
Estas 3 alturas se cortan en un punto único'' |
Estas 3 alturas se cortan en un punto único '''<math>H</math>''' llamado '''''ortocentro ''''' del triángulo. |
||
Notas: |
Notas: |
||
* Un |
* Un triángulo es rectángulo si y sólo si su ortocentro es uno de los vértices del triángulo |
||
* Un triángulo es |
* Un triángulo es obtusángulo si y sólo si su ortocentro se encuentra fuera del triángulo |
||
* Un triángulo es acutángulo si y sólo si su ortocentro está |
* Un triángulo es acutángulo si y sólo si su ortocentro está dentro del triángulo |
||
<br |
<br style="clear:both" /> |
||
=== Recta y |
=== Recta y círculo de Euler === |
||
{{AP| Recta de Euler | Círculo de Euler}} |
|||
[[Archivo: droiteEuler.png |
[[Archivo:Triangle droiteEuler.png|thumb|250 px| Recta y círculo de Euler de un triángulo.]] |
||
Los tres puntos'' |
Los tres puntos '''<math>H</math>''', '''<math>G</math>''' y '''<math>\Omega</math>''' están alineados en una línea recta llamada '''''[[recta de Euler]]''''' del triángulo y verifica la relación de Euler: |
||
: <math> \ |
: <math> \Omega H = 3 \Omega G \,</math> |
||
Por otra parte, los puntos medios de los tres lados, los tres pies de las alturas y los puntos medios de los |
Por otra parte, los puntos medios de los tres lados, los tres pies de las alturas y los puntos medios de los segmentos '''<math>[AH]</math>''', '''<math>[BH]</math>''' y '''<math>[CH]</math>''' están en un mismo círculo llamado '''''círculo de [[Euler]]''''' o ''''' círculo de los nueve puntos del triángulo'''''. |
||
<br |
<br style="clear:both" /> |
||
== En el espacio == |
|||
[[Archivo: |
[[Archivo:Oktaeder-Animation.gif|thumb|200 px|left|[[Octaedro]]; [[poliedro]] de ocho caras triángulares.]] |
||
[[Archivo: |
[[Archivo:Ikosaeder-Animation.gif|thumb|200 px|[[Icosaedro]]; poliedro de veinte caras triangulares]] |
||
El triángulo es la forma de las caras de muchos [[ |
El triángulo es la forma de las caras de muchos [[poliedro]]s regulares:[[tetraedro]] (cuatro caras que son triángulos equiláteros, es la pirámide de base triangular), [[octaedro]] (ocho caras, las pirámides de Egipto son medio-octaedros), [[icosaedro]] (veinte caras) ... |
||
<br |
<br style="clear:both" /> |
||
== Historia == |
== Historia == |
||
[[Archivo: |
[[Archivo:Egyptian A'h-mosè or Rhind Papyrus (1065x1330).png|thumb|Problemas R49-> R55 del [[papiro Rhind]].]] |
||
Ningún documento matemático del [[Imperio Antiguo de Egipto |
Ningún documento matemático del [[Imperio Antiguo de Egipto|Antiguo Imperio]] ha llegado hasta nosotros. Pero la arquitectura monumental de la ([[Dinastía III de Egipto|III Dinastía]] y la [[Dinastía IV de Egipto|IV Dinastía]] de Egipto es una prueba notable de que los egipcios de esa época tenían conocimientos relativamente sofisticados de geometría, especialmente en el estudio de los triángulos. |
||
{{AP|Gran Pirámide de Giza}} |
|||
[[Archivo: |
[[Archivo:triangle-R51-Papyrus-rhind.jpg|thumb|Figura del triángulo representada en el problema R51 del [[papiro Rhind]]]] |
||
El cálculo de la superficie de esta figura se analiza en los problemas |
El cálculo de la superficie de esta figura se analiza en los problemas R51 del [[papiro Rhind]], M4, M7 y M17 del [[papiro de Moscú]], que datan todos del [[Imperio Medio de Egipto|Imperio Medio]]. El problema R51 constituye en la historia mundial de las matemáticas, el primer testimonio escrito que trata del cálculo de la superficie de un triángulo. |
||
; |
;Enunciado del problema R51 del [[papiro Rhind]]:<ref>[[#ABC |A. Buffum Chace, ''Rhind papyrus'']], pl. 73.</ref> |
||
{{Cita|Ejemplo de cálculo de un triángulo de tierra. Si alguien te dice: un triángulo de 10 khet sobre su ''mryt'' y de 4 khet de base. ¿Cuál es su área? Calcular la mitad de 4, que es 2 para formar un rectángulo. Multiplica 10 por 2. Esta es su área.}} |
|||
El término'''' |
El término ''mryt'' significa probablemente la altura o el lado. Sin embargo, la fórmula utilizada para calcular el área hace pensar en la interpretación en favor de la primera solución.<ref>[[#CM |C. Marshall, ''Ancient Egyptian Science'']], p.70</ref>El escriba tomaba la mitad de la base del triángulo y calculaba el área del rectángulo formado por ese lado y la altura; es decir |
||
<center> |
<center><math>A = \frac{base}{2}{mryt}</math></center> |
||
equivalente a la fórmula general utilizada en nuestros días: |
equivalente a la fórmula general utilizada en nuestros días: |
||
<center> |
<center><math>S = \frac{ah}{2}</math></center> |
||
El |
El hecho de que un triángulo de lados 3-4-5 es rectángulo también era conocido por los antiguos egipcios y mesopotámicos. |
||
[[Euclides]], en el Libro I de sus''[[Elementos de Euclides |
[[Euclides]], en el Libro I de sus '' [[Elementos de Euclides|Elementos]] '', hacia el 300 antes de Cristo, enunció la propiedad de la suma de los ángulos del triángulo. |
||
== Véase también == |
== Véase también == |
||
* [[Congruencia de triángulos]] |
* [[Congruencia de triángulos]] |
||
* [[Triángulos |
* [[Triángulos semejantes]] |
||
* [[Altura de un triángulo]] |
* [[Altura de un triángulo]] |
||
* [[Vértice (geometría) |
* [[Vértice (geometría)|Vértice]] |
||
* [[Teorema de Pitágoras]] |
* [[Teorema de Pitágoras]] |
||
* [[Teorema de Tales]] |
* [[Teorema de Tales]] |
||
| Línea 313: | Línea 313: | ||
* [[Teorema del coseno]] |
* [[Teorema del coseno]] |
||
* [[Recta de Euler]] |
* [[Recta de Euler]] |
||
* [[Anexo: |
* [[Anexo:Ecuaciones de figuras geométricas]] |
||
* [[Fórmula de Herón]] |
* [[Fórmula de Herón]] |
||
* |
*[[Cateto]] |
||
Tipos de triángulos: |
Tipos de triángulos: |
||
* [[ |
* [[triángulo equilátero]], si tiene los tres ángulos y los tres lados iguales; |
||
* [[ |
* [[triángulo rectángulo]], si tiene uno de sus ángulos recto; |
||
* [[ |
* [[triángulo sagrado egipcio]], un triángulo rectángulo cuyos lados guardan la relación 3, 4, 5; |
||
* [[ |
* [[triángulo esférico]], si está contenido en una superficie esférica; |
||
* [[ |
* [[triángulo Bézier]], una superficie geométrica cuyos lados son curvas de Béizer; |
||
* [[ |
* [[triángulo de Sierpinski]], un fractal que se puede construir a partir de un triángulo. |
||
== Notas == |
== Notas == |
||
Listaref |
{{Listaref}} |
||
== Referencias == |
== Referencias == |
||
* |
* {{Traducido ref|fr|Triangle|Francés|44921774|trad=parcial}} |
||
== Enlaces externos == |
== Enlaces externos == |
||
{{commonscat|Triangles|triángulos}} |
|||
{{wikcionario|triángulo}} |
|||
((Wikcionario | Triángulo)) |
|||
[[Categoría: |
[[Categoría:Triángulos| ]] |
||
{{Destacado|ka}} |
|||
{{destacado|km}} |
|||
{{destacado|pt}} |
|||
[[an: |
[[an:Trianglo]] |
||
[[ar: |
[[ar:مثلث]] |
||
[[ |
[[arz:مثلث]] |
||
[[ast: |
[[ast:Triángulu]] |
||
[[ay: |
[[ay:Mujina]] |
||
[[az: |
[[az:Üçbucaqlar]] |
||
[[ |
[[bat-smg:Trėkompis]] |
||
[[ |
[[be:Трохвугольнік]] |
||
[[be-x-old:Трыкутнік]] |
|||
[[bg: |
[[bg:Триъгълник]] |
||
[[bn: |
[[bn:ত্রিভুজ]] |
||
[[br: |
[[br:Tric'horn]] |
||
[[bs: |
[[bs:Trougao]] |
||
[[ca: |
[[ca:Triangle]] |
||
[[ |
[[ckb:سێگۆشە]] |
||
[[co: |
[[co:Triangulu]] |
||
[[cs: |
[[cs:Trojúhelník]] |
||
[[cv: |
[[cv:Виç кĕтеслĕх]] |
||
[[cy: |
[[cy:Triongl]] |
||
[[da: |
[[da:Trekant]] |
||
[[de: |
[[de:Dreieck]] |
||
[[el: |
[[el:Τρίγωνο]] |
||
[[en: |
[[en:Triangle]] |
||
[[eo: |
[[eo:Triangulo]] |
||
[[et: |
[[et:Kolmnurk]] |
||
[[ |
[[eu:Hiruki]] |
||
[[fa: |
[[fa:مثلث]] |
||
[[fi: |
[[fi:Kolmio]] |
||
[[fr: |
[[fr:Triangle]] |
||
[[ga: |
[[ga:Triantán]] |
||
[[gl: |
[[gl:Triángulo]] |
||
[[ |
[[he:משולש]] |
||
[[hr: |
[[hr:Trokut]] |
||
[[hsb: |
[[hsb:Třiróžk]] |
||
[[ |
[[ht:Triyang]] |
||
[[hu: |
[[hu:Háromszög]] |
||
[[hy: |
[[hy:Եռանկյուն]] |
||
[[id: |
[[id:Segitiga]] |
||
[[io: |
[[io:Triangulo]] |
||
[[ |
[[is:Þríhyrningur]] |
||
[[it: |
[[it:Triangolo]] |
||
[[ja:三角形]] |
[[ja:三角形]] |
||
[[ka: |
[[ka:სამკუთხედი]] |
||
[[km: |
[[km:ត្រីកោណ]] |
||
[[ko: |
[[ko:삼각형]] |
||
[[ku: |
[[ku:Sêgoşe]] |
||
[[la: |
[[la:Triangulum]] |
||
[[li: |
[[li:Driehook]] |
||
[[lo: |
[[lo:ຮູບສາມແຈ]] |
||
[[lt: |
[[lt:Trikampis]] |
||
[[lv: |
[[lv:Trīsstūris]] |
||
[[mk: |
[[mk:Триаголник]] |
||
[[ml: |
[[ml:ത്രികോണം]] |
||
[[ |
[[mn:Гурвалжин]] |
||
[[ |
[[mr:त्रिकोण]] |
||
[[ms: |
[[ms:Segi tiga]] |
||
[[ |
[[new:त्रिकोण]] |
||
[[nl: |
[[nl:Driehoek (meetkunde)]] |
||
[[nn: |
[[nn:Trekant]] |
||
[[no: |
[[no:Trekant]] |
||
[[nrm: |
[[nrm:Trian]] |
||
[[pl: |
[[pl:Trójkąt]] |
||
[[pt: |
[[pt:Triângulo]] |
||
[[qu: |
[[qu:Kimsak'uchu]] |
||
[[ro: |
[[ro:Triunghi]] |
||
[[ru: |
[[ru:Треугольник]] |
||
[[scn: |
[[scn:Triànculu]] |
||
[[sco: |
[[sco:Triangle]] |
||
[[sh: |
[[sh:Trokut]] |
||
[[simple: |
[[simple:Triangle]] |
||
[[sk: |
[[sk:Trojuholník]] |
||
[[ |
[[sl:Trikotnik]] |
||
[[sq: |
[[sq:Trekëndëshi]] |
||
[[sr: |
[[sr:Троугао]] |
||
[[su: |
[[su:Juru tilu]] |
||
[[sv: |
[[sv:Triangel]] |
||
[[ |
[[sw:Pembetatu]] |
||
[[ta: |
[[ta:முக்கோணம்]] |
||
[[te: |
[[te:త్రిభుజం]] |
||
[[ |
[[tg:Секунҷа]] |
||
[[th: |
[[th:รูปสามเหลี่ยม]] |
||
[[tl: |
[[tl:Tatsulok]] |
||
[[tr: |
[[tr:Üçgen]] |
||
[[uk: |
[[uk:Трикутник]] |
||
[[ |
[[ur:مثلث]] |
||
[[uz: |
[[uz:Uchburchak]] |
||
[[vi: |
[[vi:Tam giác]] |
||
[[vls: |
[[vls:Drieoek]] |
||
[[ |
[[war:Triangulo]] |
||
[[yi: |
[[yi:דרייעק]] |
||
[[yo: |
[[yo:Anígunmẹ́ta]] |
||
[[zh:三角形]] |
[[zh:三角形]] |
||
[[zh-classical:三角形]] |
|||
[[zh-min-nan: |
[[zh-min-nan:Saⁿ-kak-hêng]] |
||
[[zh-yue:三角形]] |
[[zh-yue:三角形]] |
||
Revisión del 17:40 16 feb 2010

Un triángulo, geométricamente hablando, es un polígono determinado por tres rectas que se cortan dos a dos en tres puntos (que no se encuentran alineados). Los puntos de intersección de las rectas son los vértices y los segmentos de recta determinados son los lados del triángulo. Dos lados contiguos forman uno de los ángulos interiores del triángulo.
Por lo tanto, un triángulo tiene 3 elementos: 3 ángulo interiores, 3 lados y 3 vértices.
Si está contenido en una superficie plana se denomina triángulo, o trígono, un nombre menos común para este tipo de polígonos. Si está contenido en una superficie esférica se denomina triángulo esférico. Representado, en cartografía, sobre la superficie terrestre, se llama triángulo geodésico.
Convención de escritura

Los puntos principales de una figura geométrica, como los vértices de un polígono, suelen ser designados por letras latinas mayúsculas: A, B, C, ...
Un triángulo se nombra entonces como cualquier otro polígono, nombrando sucesivamente sus vértices, por ejemplo ABC. El orden de citación de los vértices es irrelevante, porque todos los segmentos de los que estos vértices son los extremos, son los lados del triángulo.
Los lados del triángulo, son llamados, como todos los segmentos, por sus extremos: AB, BC y AC, en nuestro ejemplo.
Para nombrar la longitud de un lado, por lo general se utiliza el nombre del vértice opuesto, convertido a minúscula latina: para BC, para AC, para AB.
La notación general para el ángulo entre dos segmentos OP y OQ que comparten el extremo O es
También podemos utilizar una letra minúscula, griega lo más a menudo, coronada por un acento circunflejo (en rigor, los ángulos deben ser designados por letras mayúsculas y su medida por minúsculas, pero a menudo se utilizan los mismos nombres para los dos con el fin de simplificar la notación). En el caso de un triángulo, el ángulo entre dos lados todavía puede, por tolerancia y en ausencia de ambigüedad, ser designado por el nombre del vértice común, coronado por un acento circunflejo. En resumen, en nuestro ejemplo, podemos observar los ángulos:
Clasificación de los triángulos
Los triángulos se pueden clasificar por la longitud de sus lados o por la amplitud de sus ángulos.
Por la longitud de sus lados
Por la longitud de sus lados, los triángulos se clasifican en:
- Triángulo equilátero: si sus tres lados tienen la misma longitud (los tres ángulos internos miden 60 grados ó radianes.)
- Triángulo isósceles: si tiene dos lados de la misma longitud. Los ángulos que se oponen a estos lados tienen la misma medida.
- Triángulo escaleno: si todos sus lados tienen longitudes diferentes. En un triángulo escaleno no hay ángulos con la misma medida.

|

|

|
| Equilátero | Isósceles | Escaleno |
Por la amplitud de sus ángulos
Por la amplitud de sus ángulos, los triángulos se clasifican en:
- Triángulo rectángulo: si tiene un ángulo interior recto (90°). A los dos lados que conforman el ángulo recto se les denomina catetos y al otro lado hipotenusa.
- Triángulo obtusángulo: si uno de sus ángulos es obtuso (mayor de 90°); los otros dos son agudos (menor de 90°).
- Triángulo acutángulo: cuando sus tres ángulos son menores a 90°; el triángulo equilátero es un caso particular de triángulo acutángulo.

|

|

|
| Rectángulo | Obtusángulo | Acutángulo |
| Oblicuángulos | ||
Se llama triángulo oblicuángulo cuando ninguno de sus ángulos interiores son rectos (90°). Por ello, los triángulos obtusángulos y acutángulos son oblicuángulos.
Clasificación según los lados y los ángulos
Los triángulos acutángulos pueden ser:
- Triángulo acutángulo isósceles: con todos los ángulos agudos, siendo dos iguales, y el otro distinto, este triángulo es simétrico respecto de su altura.
- Triángulo acutángulo escaleno: con todos sus ángulos agudos y todos diferentes, no tiene eje de simetría.
- Triángulo acutángulo equilátero: sus tres lados y sus tres ángulos son iguales; las tres alturas son ejes de simetría (dividen al triángulo en dos triángulos iguales).
Los triángulos rectángulos pueden ser:
- Triángulo rectángulo isósceles: con un angulo recto y dos agudos iguales (de 45° cada uno), dos lados son iguales y el otro diferente: los lados iguales son los catetos y el diferente es la hipotenusa. Es simétrico respecto a la altura de la hipotenusa, que pasa por el ángulo recto.
- Triángulo rectángulo escaleno: tiene un ángulo recto, y todos sus lados y ángulos son diferentes.
Los triángulos obtusángulos pueden ser:
- Triángulo obtusángulo isósceles: tiene un ángulo obtuso, y dos lados iguales que son los que forman el ángulo obtuso; el otro lado es mayor que éstos dos.
- Triángulo obtusángulo escaleno: tiene un ángulo obtuso y todos sus lados son diferentes.
| Triángulo | equilátero | isósceles | escaleno |
|---|---|---|---|
| acutángulo | 
|

|

|
| rectángulo | 
|

| |
| obtusángulo | 
|

|
Congruencia de triángulos
Dos triángulos son congruentes si hay una correspondencia entre sus vértices de tal manera que el ángulo del vértice y los lados que lo componen sean congruentes con los del otro triángulo.
Postulados de congruencia
Semejanza de triángulos
Dos triángulos son semejantes si sus ángulos tienen la misma amplitud y los lados opuestos de estos ángulos son proporcionales.
- Criterio aa (ángulo, ángulo). Si dos de sus ángulos son semejantes
- Criterio lal (lado, ángulo, lado). Si dos de sus lados son proporcionales y el ángulo comprendido entre ellos es congruente.
- Criterio lll (lado, lado, lado). Si sus tres lados son proporcionales.
Semejanzas de triángulos rectángulos
Dos triángulos rectángulos son semejantes si cumple con al menos uno de los criterios siguientes:
- Si uno tiene un ángulo agudo de igual amplitud que un ángulo agudo del otro.
- Si uno tiene los dos catetos proporcionales con los del otro.
- Si uno tiene un cateto y la hipotenusa proporcionales con los del otro.
Propiedades de los triángulos


Un triángulo puede ser definido como un polígono de tres lados, o como un polígono con tres vértices.
Después del punto y el segmento, el triángulo es el polígono más simple. Es el único que no tiene diagonal. En el espacio, tres puntos definen un triángulo (y un plano). Por el contrario, si cuatro puntos de un mismo plano forman un cuadrilátero, cuatro puntos que no estén en el mismo plano no definen un polígono, sino un tetraedro
Por otra parte, cada polígono puede ser dividido en un número finito de triángulos que se forman con una triangulación del polígono. El número mínimo de triángulos necesarios para esta división es , donde n es el número de lados del polígono. El estudio de los triángulos es fundamental para el estudio de otros polígonos, por ejemplo para la demostración del Teorema de Pick.

- Los tres ángulos internos de un triángulo miden 180° lo que equivale a π radianes, en geometría euclidiana.[1]

Euclides había demostrado este resultado en sus Elementos (proposición I-32) de la siguiente manera: trazamos la paralela a la línea (AB) que pasa por C. Siendo paralelas, esta recta y la recta (AB) forman con la recta (AC) ángulos iguales, codificados en color rojo en la figura de al lado (ángulos alternos-internos). Del mismo modo, los ángulos codificados en color azul son iguales (ángulos correspondientes). Por otro lado, la suma de los tres ángulos del vértice C es el ángulo llano. Así que la suma de las medidas del ángulo de color rojo, del ángulo verde y del azul es un ángulo de 180 ° (o π radianes). La suma de los ángulos de un triángulo es 180 °.
Esta propiedad es el resultado de la geometría euclidiana. No se verifica en general en la geometría no euclidiana.
- La suma de las longitudes de dos de sus lados es siempre mayor que la longitud del tercer lado.
- El valor de la paralela media de un triángulo (recta que une dos puntos medios de dos lados) es igual a la mitad del lado paralelo.
- Para cualquier triángulo se verifica el Teorema del seno que establece: «Los lados de un triángulo son proporcionales a los senos de los ángulos opuestos»:

- Para cualquier triángulo se verifica el Teorema del coseno que demuestra que «El cuadrado de un lado es igual a la suma de los cuadrados de los otros lados menos el doble del producto de estos lados por el coseno del ángulo comprendido»:
- Para cualquier triángulo rectángulo, cuyos catetos miden a y b, y cuya hipotenusa mida c, se verifica el Teorema de Pitágoras:
Centros del triángulo
Geométricamente se pueden definir varios centros en un triángulo:
- Baricentro: es el punto que se encuentra en la intersección de las medianas, y equivale al centro de gravedad
- Circuncentro: es el centro de la circunferencia circunscrita, aquella que pasa por los tres vértices del triángulo. Se encuentra en la intersección de las mediatrices de los lados. Además, la circunferencia circunscrita contiene los puntos de intersección de la mediatriz de cada lado con las bisectrices que pasan por el vértice opuesto.
- Incentro: es el centro de la circunferencia inscrita, aquella que es tangente a los lados del triángulo. Se encuentra en la intersección de las bisectrices de los ángulos.
- Ortocentro: es el punto que se encuentra en la intersección de las alturas.
- Exincentros: son los centros de las circunferencias exinscritas, aquellas que son tangentes a los lados del triángulo. Se encuentra en la intersección de una bisectriz interior y dos bisectrices exteriores de los ángulos.
El único caso en que los cuatro primeros centros coinciden en un único punto es en un triángulo equilátero.
Cálculo de elementos en un triángulo
Para resolver triángulos utilizamos generalmente el Teorema de Pitágoras cuando son triángulos rectángulos, o los Teoremas del seno y del coseno.
Elementos notables de un triángulo
Medianas y centro de gravedad

Se lama mediana de un triángulo cada una de las tres líneas que pasan por un vértice del triángulo y por el punto medio del lado opuesto al vértice.
Cada una de las tres medianas dividen el triángulo en dos triángulos de áreas iguales.
Las tres medianas de un triángulo son concurrentes. Su punto de intersección es llamado centro de gravedad del triángulo.
Mediatrices y círculo circunscrito

Se llama mediatriz de un triángulo a cada una de las mediatrices de sus lados , et .
Las tres mediatrices de un triángulo son concurrentes en un punto equidistante de los tres vértices. El círculo de centro y radio que pasa por cada uno de los tres vértices del triángulo es el círculo circunscrito al triángulo.
Notas:
- Un triángulo es obtusángulo si y sólo si las bisectrices se cortan fuera del triángulo.
- Un triángulo es acutángulo si y sólo si las bisectrices se cortan dentro del triángulo.
Propiedad:
- es un triángulo rectángulo en si y sólo si el centro de su círculo circunscrito es el centro de .
Bisectriz y círculo inscrito

Las bisectrices de un triángulo son las tres bisectrizes de sus ángulos internos.
Las tres bisectrices de un triángulo son concurrentes en un punto O. El círculo inscrito del triángulo es el único círculo tangente a los tres lados del triángulo y está totalmente incluido en el triángulo. Tiene por punto central O, que es pues el centro del círculo inscrito en el triángulo.
Alturas y ortocentro

Se llama altura de un triángulo a cada una de las tres líneas que pasan por un vértice del triángulo y son perpendiculares a la cara opuesta al vértice. La intersección de la altura y el lado opuesto se denomina «pie» de la altura.
Estas 3 alturas se cortan en un punto único llamado ortocentro del triángulo.
Notas:
- Un triángulo es rectángulo si y sólo si su ortocentro es uno de los vértices del triángulo
- Un triángulo es obtusángulo si y sólo si su ortocentro se encuentra fuera del triángulo
- Un triángulo es acutángulo si y sólo si su ortocentro está dentro del triángulo
Recta y círculo de Euler

Los tres puntos , y están alineados en una línea recta llamada recta de Euler del triángulo y verifica la relación de Euler:
Por otra parte, los puntos medios de los tres lados, los tres pies de las alturas y los puntos medios de los segmentos , y están en un mismo círculo llamado círculo de Euler o círculo de los nueve puntos del triángulo.
En el espacio

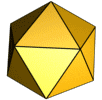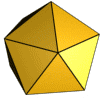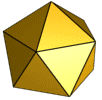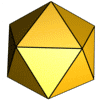
El triángulo es la forma de las caras de muchos poliedros regulares:tetraedro (cuatro caras que son triángulos equiláteros, es la pirámide de base triangular), octaedro (ocho caras, las pirámides de Egipto son medio-octaedros), icosaedro (veinte caras) ...
Historia

Ningún documento matemático del Antiguo Imperio ha llegado hasta nosotros. Pero la arquitectura monumental de la (III Dinastía y la IV Dinastía de Egipto es una prueba notable de que los egipcios de esa época tenían conocimientos relativamente sofisticados de geometría, especialmente en el estudio de los triángulos.

El cálculo de la superficie de esta figura se analiza en los problemas R51 del papiro Rhind, M4, M7 y M17 del papiro de Moscú, que datan todos del Imperio Medio. El problema R51 constituye en la historia mundial de las matemáticas, el primer testimonio escrito que trata del cálculo de la superficie de un triángulo.
- Enunciado del problema R51 del papiro Rhind
- [2]
Ejemplo de cálculo de un triángulo de tierra. Si alguien te dice: un triángulo de 10 khet sobre su mryt y de 4 khet de base. ¿Cuál es su área? Calcular la mitad de 4, que es 2 para formar un rectángulo. Multiplica 10 por 2. Esta es su área.
El término mryt significa probablemente la altura o el lado. Sin embargo, la fórmula utilizada para calcular el área hace pensar en la interpretación en favor de la primera solución.[3]El escriba tomaba la mitad de la base del triángulo y calculaba el área del rectángulo formado por ese lado y la altura; es decir
equivalente a la fórmula general utilizada en nuestros días:
El hecho de que un triángulo de lados 3-4-5 es rectángulo también era conocido por los antiguos egipcios y mesopotámicos.
Euclides, en el Libro I de sus Elementos , hacia el 300 antes de Cristo, enunció la propiedad de la suma de los ángulos del triángulo.
Véase también
- Congruencia de triángulos
- Triángulos semejantes
- Altura de un triángulo
- Vértice
- Teorema de Pitágoras
- Teorema de Tales
- Teorema del cateto
- Teorema del seno
- Teorema del coseno
- Recta de Euler
- Anexo:Ecuaciones de figuras geométricas
- Fórmula de Herón
- Cateto
Tipos de triángulos:
- triángulo equilátero, si tiene los tres ángulos y los tres lados iguales;
- triángulo rectángulo, si tiene uno de sus ángulos recto;
- triángulo sagrado egipcio, un triángulo rectángulo cuyos lados guardan la relación 3, 4, 5;
- triángulo esférico, si está contenido en una superficie esférica;
- triángulo Bézier, una superficie geométrica cuyos lados son curvas de Béizer;
- triángulo de Sierpinski, un fractal que se puede construir a partir de un triángulo.
Notas
- ↑ En la geometría no euclidiana, como la de Riemann y Lobachevsky la suma de los ángulos internos es diferente a 180°.
- ↑ A. Buffum Chace, Rhind papyrus, pl. 73.
- ↑ C. Marshall, Ancient Egyptian Science, p.70
Referencias
- Esta obra contiene una traducción parcial derivada de «Triangle» de Wikipedia en francés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.Error: número de versión no válido.
Enlaces externos
 Wikimedia Commons alberga una categoría multimedia sobre triángulos.
Wikimedia Commons alberga una categoría multimedia sobre triángulos. Wikcionario tiene definiciones y otra información sobre triángulo.
Wikcionario tiene definiciones y otra información sobre triángulo.


















![{\displaystyle [AB]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13e80b9404482bdbe7fe18d8435b3dd42fd39bb0)
![{\displaystyle [AC]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49b377aec839d74e0b48a42d2ba192d3efefc575)
![{\displaystyle [BC]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd2ee765006b05ac0001c01a206871306f108cbc)






![{\displaystyle [AH]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98621a04b0a0b00e439c7cda9894bf1e184781bf)
![{\displaystyle [BH]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2f58a4ff7ecbc9c1f643ed7500daba1612c57b4)
![{\displaystyle [CH]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49f6a126a2744c5e2e4a216010592f61ba749447)

