Teorema del coseno

Fig. 1 - Notaciones habituales en un triángulo cualquiera.

El teorema del coseno es un teorema comúnmente utilizado en trigonometría. Es la generalización del teorema de Pitágoras en los triángulos no rectángulos: relaciona el tercer lado de un triángulo con los dos primeros y con el coseno del ángulo formado por estos dos lados.

Sea un triángulo ABC, en el cual utilizamos las notaciones habituales expuestas en la figura 1: por una parte α, β y γ para los ángulos y, por otra parte, a, b y c para los lados respectivamente opuestos a estos ángulos. Entonces, el teorema del coseno se enuncia de la siguiente manera:

$\,c^{2}=a^{2}+b^{2}-2ab\cos \gamma$

En la mayoría de los idiomas, este teorema es conocido con el nombre de teorema del coseno, denominación no obstante relativemente tardía. En francés, sin embargo, lleva el nombre del matemático persa Ghiyath al-Kashi que unificó los resultados de sus predecesores.

Historia

Fig. 2 - Triángulo ABC con altura BH

Los Elementos de Euclides, que datan del siglo III adC, contienen ya una aproximación geométrica de la generalización del teorema de Pitágoras: las proposiciones 12 y 13 del libro II, tratan separadamente el caso de un triángulo obtusángulo y el de un triángulo acutángulo. La formulación de la época es pedestre ya que la ausencia de funciones trigonométricas y del álgebra obliga a razonar en términos de diferencias de áreas. Por eso, la proposición 12 utiliza estos términos:

«En los triángulos obtusángulos, el cuadrado del lado opuesto al ángulo obtuso es mayor que los cuadrados de los lados que comprenden el ángulo obtuso en dos veces el rectángulo comprendido por un lado de los del ángulo obtuso sobre el que cae la perpendicular y la recta exterior cortada por la perpendicular, hasta el ángulo obtuso.»

Euclides, Elementos.​

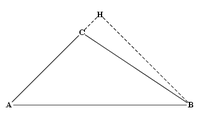
Y señalando ABC el triángulo de ángulo obtuso A y H el pie de la altura resultante de B (cf. Fig. 2 contigua), las notaciones modernas permiten resumir el enunciado así:

$AB^{2}=CA^{2}+CB^{2}+2\ CA\ CH.$

Faltaba esperar la trigonometría árabe-musulmana de la Edad Media para ver al teorema evolucionar a su forma y en su alcance: el astrónomo y matemático al-Battani​ generalizó el resultado de Euclides en la geometría esférica a principios del siglo X, lo que permitió efectuar los cálculos de la distancia angular entre las estrellas. Fue durante el mismo período cuando se establecieron las primeras tablas trigonométricas, para las funciones seno y coseno. Eso permitió a Ghiyath al-Kashi,​ matemático de la escuela de Samarcanda, de poner el teorema bajo una forma utilizable para la triangulación durante el siglo XV. La propiedad fue popularizada en occidente por François Viète quien, al parecer, lo redescubrió independientemente.

Fue a principio del siglo XIX cuando las notaciones algebraicas modernas permitieron escribir el teorema bajo su forma actual y cuando tomó en numerosos idiomas el nombre de teorema (o ley) del coseno.

El teorema y sus aplicaciones

El teorema del coseno es también conocido por el nombre de teorema de Pitágoras generalizado, ya que el teorema de Pitágoras es un caso particular: cuando el ángulo $\gamma$ es recto, o dicho de otro modo cuando $\cos \gamma =0$, el teorema del coseno se escribe

$\,c^{2}=a^{2}+b^{2}$,

y recíprocamente.

Fig. 3 - Utilización del teorema del coseno: ángulo o lado desconocido.

El teorema se utiliza en triangulación (ver Fig. 3) para resolver un triángulo, saber determinar

• el tercer lado de un triángulo donde conocemos un ángulo y los lados adyacentes:

$\,c={\sqrt {a^{2}+b^{2}-2ab\cos \gamma }}$ ;

• los ángulos de un triángulo donde conocemos los tres lados:

$\,\gamma =\arccos {\frac {a^{2}+b^{2}-c^{2}}{2ab}}$.

Hace falta señalar que estas fórmulas son numéricamente inestables en el caso de triángulos en alfiler, es decir cuando c es pequeña frente a y b — o, de manera equivalente, cuando γ es pequeña frente 1.

Existe un corolario del teorema del coseno: para dos triángulos directamente semejantes ABC y A'B'C'

$\,cc'=aa'+bb'-(ab'+a'b)\cos \gamma$.

Demostraciones

Por desglose de áreas

Un cierto número de la demostraciones del teorema hacen intervenir un cálculo de áreas. Conviene en efecto remarcar que

• $a^{2}$, $b^{2}$ y $c^{2}$ son las áreas de los cuadrados de lados respectivos $a$, $b$ y $c$ ;
• $ab|\cos \gamma |$ es de un paralelogramo de lados $a$ y $b$ formando un ángulo $\pi /2-\gamma$, el cambio de signo de $\cos \gamma$ cuando el ángulo $\gamma$ se vuelve obtuso debe un estudio por caso obligatorio.

Fig. 4a - Demostración del teorema del coseno por los triángulos de ángulos agudos: « método de desglose ».

La figura 4a (contigua) desglosa un heptágono de dos maneras diferentes para salir a demostrar el teorema del coseno en el caso de un ángulo agudo. Interviennent :

• en rosa, las áreas $a^{2}$, $b^{2}$ a la izquierda, y las áreas $2ab\cos \gamma$ y $c^{2}$ a la derecha;
• en azul, el triángulo ABC, tanto a derecha como a izquierda;
• en gris, algunos triángulos suplementarios, idénticos al triángulo ABC y en el mismo número dentro de los dos desgloses.

La igualdad de las áreas de derecha y izquierda da

$\,a^{2}+b^{2}=c^{2}+2ab\cos \gamma$.

Fig. 4b - Demostración del teorema del coseno en el caso de un ángulo obtuso: « método de desglose »

La figura 4b (contigua) desglosa un hexágono de dos maneras diferentes para salir a demostrar el terorema del coseno en el caso de un ángulo obtuso. La figura muestra

• en rosa, las áreas $a^{2}$, $b^{2}$ y $-2ab\cos \gamma$ a la izquierda, y las áreas $c^{2}$ a la derecha;
• en azul, dos veces el triángulo ABC, tanto a la derecha como a la izquierda.

La igualdad de las áreas a derecha y izquierda da

$\,a^{2}+b^{2}-2ab\cos \gamma =c^{2}$.

Una demostración rigurosa necesitar probar que los dos desgloses son efectivamente idénticos, lo que se utiliza principalmente en el caso de igualdad de los triángulos.

Por el teorema de Pitágoras

Notemos que el Teorema de Cosenos es equivalente al Teorema de Pitágoras cuando el ángulo $\gamma$ es recto. Hay dos casos a considerar: cuando c es un lado de un ángulo obtuso y cuando no lo es.

Primer caso: c es adyacente a dos ángulos agudos.

Caso 1: c es adyacente a dos ángulos agudos

Consideremos la figura adjunta. El teorema de Pitágoras establece que:

$c^{2}=h^{2}+u^{2}\,$

$h^{2}=a^{2}-(b-u)^{2}\,$

Combinando ambas ecuaciones y luego simplificando obtenemos

$c^{2}=u^{2}+a^{2}-b^{2}+2bu-u^{2}\,$

$c^{2}=a^{2}-b^{2}+2bu\,$

Usando la definición de coseno, se tiene

$\cos \gamma ={\frac {b-u}{a}}\,$

y por tanto

$u=b-a\,\cos \gamma \,$

Sustituimos el valor de u en la expresión para c² y simplificamos:

$c^{2}=a^{2}-b^{2}+2b\,(b-a\,\cos \gamma )$

$c^{2}=a^{2}+b^{2}-2ab\,\cos \gamma$

terminando con esto la prueba del primer caso.

Segundo caso: c es adyacente a un ángulo obtuso.

Caso 2: c es adyacente a un ángulo obtuso

Consideremos la figura adjunta. El teorema de Pitágoras establece que:

$c^{2}=h^{2}+u^{2}\,$

$h^{2}=a^{2}-(b+u)^{2}\,$

Combinando ambas ecuaciones obtenemos

$c^{2}=u^{2}+a^{2}-b^{2}-2bu-u^{2}=a^{2}-b^{2}-2bu\,$

Usando la definición de coseno, se tiene

$\cos \gamma ={\frac {b+u}{a}}$

y por tanto

$u=a\,\cos \gamma -b\,$

Sustituimos en la expresión para c² y simplificamos:

$c^{2}=a^{2}-b^{2}-2b\,(a\,\cos \gamma -b)\,$

$c^{2}=a^{2}+b^{2}-2ab\,\cos \gamma \,$

y esto concluye la demostración.

Es importante notar, que si se considera a u como un segmento dirigido, entonces sólo hay un caso y las dos demostraciones se convierten en la misma.

Por la potencia de un punto con respecto a un círculo

Fig. 6 - Demostración del teorema del coseno utilizando la potencia de un punto con respecto a un círculo.

Consideramos el círculo de centro B y de radio [BC](figura 6). Corta a la derecha (AC) en C y K. La potencia del punto A con respecto a dicho círculo es

$\mathrm {AB} ^{2}-\mathrm {BC} ^{2}\,$	$={\overline {\mathrm {AC} }}\cdot {\overline {\mathrm {AK} }}$
	$={\overline {\mathrm {AC} }}\cdot ({\overline {\mathrm {AC} }}+{\overline {\mathrm {CK} }})$
$c^{2}-a^{2}\,$	$=b\,(b-2a\cos \gamma )$.

Contrariamente a las precedentes, para esta demostración, no es necesario recurrir a un estudio por caso. En efecto, las medidas algebraicas permiten tratar paralelamente un ángulo agudo (${\overline {\mathrm {CK} }}<0$) y un ángulo obtuso (${\overline {\mathrm {CK} }}>0$).

Por el cálculo vectorial

Utilizando el cálculo vectorial, más precisamente el producto escalar, es posible encontrar el teorema del coseno en algunas líneas:

$c^{2}\,$	$=\lVert {\overrightarrow {\mathrm {AB} }}\lVert ^{2}$
	$=\lVert {\overrightarrow {\mathrm {CB} }}-{\overrightarrow {\mathrm {CA} }}\lVert ^{2}$
	$=\lVert {\overrightarrow {\mathrm {CB} }}\lVert ^{2}-2\cdot {\overrightarrow {\mathrm {CB} }}\cdot {\overrightarrow {\mathrm {CA} }}+\lVert {\overrightarrow {\mathrm {CA} }}\lVert ^{2}$
	$=\mathrm {CB} ^{2}-2\cdot \left|\mathrm {CB} \right|\cdot \left|\mathrm {CA} \right|\cos {\widehat {\mathrm {ACB} }}+\mathrm {CA} ^{2}$
	$=a^{2}+b^{2}-2ab\cos \gamma \,$

Generalización en geometrías no euclídeas

Fig. 7 - Triángulo esférico: dimensiones reducidas a, b y c ; ángulos α, β y γ.

Para una superficie no euclídea de curvatura K, señalamos con R el radio de curvatura. Este verifica

$\,R=1/{\sqrt {|K|}}$.

Definimos entonces las dimensiones reducidas del triángulo:

$\,a=BC/R$,

$\,b=AC/R$,

$\,c=AB/R$.

En el caso de un triángulo esférico, a, b y c corresponden a la medida angular de los segmentos de grande arco [BC], [AC] y [AB] (ver Fig. 7).

Geometría esférica

Dentro de un triángulo esférico ABC (Fig. 7), el teorema del coseno se escribe

$\cos c=\cos a\,\cos b+\sin a\,\sin b\,\cos \gamma$.

Cuando el radio de curvatura es muy grande comparado con las dimensiones del triángulo, es decir cuando

$\,a<\!\!<1$,

esta expresión se simplifica para dar la versión euclídea del teorema del coseno. Para hacelo, utilizamos el desarrollo de Taylor siguiente:

$\,\sin a=a+O(a^{3})$, etc.,

$\,\cos a=1-a^{2}/2+O(a^{3})$, etc.

Existe una identidad similar que relaciona los tres ángulos:

$\cos \gamma =-\cos \alpha \,\cos \beta +\sin \alpha \,\sin \beta \,\cos c$

Geometría hiperbólica

En un triángulo hiperbólico ABC, el teorema del coseno se escribe

$\cosh c=\cosh a\,\cosh b+\sinh a\,\sinh b\,\cos \gamma$.

Cuando el radio de curvatura se vuelve muy grande frente las dimensiones del triángulo, encontramos el teorema del coseno euclídeo a partir de los desarrollos limitados

$\,\sinh a=a+O(a^{3})$, etc.,

$\,\cosh a=1+a^{2}/2+O(a^{3})$, etc.

Generalización en el espacio euclídeo

Consideramos un tetraedro A₁A₂A₃A₄ del espacio euclídeo. La figure 8 contigua presenta las notaciones cercernientes los vértices, caras y ángulos del tetraedro:

Fig. 8 - Tetraedro : caras y ángulos dibujados.

• $\,\mathrm {S} _{k}$ la cara opuesta al vértice $\mathrm {A} _{k}\$;
• $\,s_{k}$ la superficie de $\mathrm {S} _{k}\$;
• $\,\Delta _{k}$ el plano que contiene a la cara $\mathrm {S} _{k}\$;
• $\,\theta _{ij}$ el ángulo diedral ${\widehat {(\Delta _{i},\Delta _{j})}}$.

Entonces, las surperficies y ángulos verifican:

$\,s_{4}^{2}=$	$s_{1}^{2}+s_{2}^{2}+s_{3}^{2}-2s_{1}s_{2}\cos \theta _{12}\,$
	$-2s_{1}s_{3}\cos \theta _{13}-2s_{2}s_{3}\cos \theta _{23}\,$.

Véase también

• Trigonometría
  • Triangulación
  • Trigonometría esférica
  • Función trigonométrica
• Geometría del triángulo
  • Teorema de Pitágoras
  • Teorema del seno
• Matemáticos
  • Euclides
  • al-Battani
  • Ghiyath al-Kashi
  • François Viète

Bibliografía

• Elementos, tomo II, Euclides, en http://www.euclides.org/.
• Law of cosines, en Math World (en inglés)
• Géométrie Supérieure, N. Éfimov, Moscou, Editions MIR, 1981
• Petite Encyclopédie des Mathématiques, Paris, Editions K. Pagoulatos, 1980