Valor absoluto

En matemáticas, el valor absoluto o módulo​ de un número real $x$, denotado por $|x|$, es el valor de $x$ sin considerar el signo, sea este positivo o negativo.​ Por ejemplo, el valor absoluto de $3$ es $3$ y el valor absoluto de $-3$ es $3$. Algunos autores extienden la noción de valor absoluto a los números complejos, donde el valor absoluto coincide con el módulo.

El valor absoluto está vinculado con las nociones de magnitud, distancia y norma en diferentes contextos matemáticos y físicos. El concepto de valor absoluto de un número real puede generalizarse a muchos otros objetos matemáticos, como son los cuaterniones, anillos ordenados, cuerpos o espacios vectoriales.

Gráfica de la función valor absoluto.

Definición

Números reales

Para cualquier número real $x$, el valor absoluto o módulo de $x$ se denota por $|x|$ y se define como:​

$|x|=\left\{{\begin{array}{rcl}x,&{\mbox{si}}&x\geq 0\\-x,&{\mbox{si}}&x<0\end{array}}\right.$

El valor absoluto de $x$ es siempre un número positivo o cero pero nunca negativo: cuando $x$ es un número negativo $(x<0)$ entonces su valor absoluto es necesariamente positivo $(|x|=-x>0)$.

Desde un punto de vista geométrico, el valor absoluto de un número real puede verse como la distancia que existe entre ese número y el cero. De manera general, el valor absoluto de la diferencia entre dos números es la distancia entre ellos.

Propiedades

El valor absoluto tiene las siguientes cuatro propiedades fundamentales, considere $a,b\in \mathbb {R}$ entonces

${\begin{aligned}&|a|\geq 0&{\text{No-negatividad}}\\&|a|=0\iff a=0&{\text{Definición positiva}}\\&|ab|=|a||b|&{\text{Propiedad multiplicativa}}\\&|a+b|\leq |a|+|b|&{\text{Desigualdad triangular}}\end{aligned}}$

Otras propiedades útiles son las siguientes

${\begin{aligned}&||a||=|a|\\&|-a|=|a|\\&|a-b|=0\iff a=b\\&|a-b|\leq |a-c|+|c-b|\\&\left|{\frac {a}{b}}\right|={\frac {|a|}{|b|}}\quad {\text{si }}b\neq 0\\&|a-b|\geq ||a|-|b||\end{aligned}}$

estas son consecuencia de la definición o de las primeras cuatro propiedades.

Otras dos propiedades que utilizan desigualdades son

${\begin{aligned}&|a|\leq b\iff -b\leq a\leq b\\&|a|\geq b\iff a\leq -b\quad {\mbox{o}}\quad a\geq b\end{aligned}}$

Estas relaciones pueden ser utilizadas para resolver desigualdades que involucran el valor absoluto, por ejemplo:

${\begin{aligned}|x-3|\leq 9&\iff -9\leq x-3\leq 9\\&\iff -6\leq x\leq 12\end{aligned}}$

Definición equivalente

Si $x$ es un número real, su valor absoluto es un número real no negativo definido de las dos siguientes maneras:

1. $|x|={\sqrt {x^{2}}}$
2. $|x|$ es igual al máximo de $\{-x,x\}$.​

Función Valor absoluto

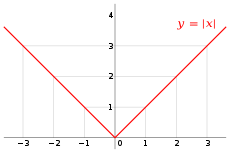
La función real valor absoluto se define sobre el conjunto de todos los números reales asignando a cada número real su respectivo valor absoluto.

Formalmente, el valor absoluto de todo número real $x\,$ está definido por:​

${\begin{aligned}|\quad |:\mathbb {R} &\to \mathbb {R} ^{+}\cup \{0\}\\x&\mapsto |x|\end{aligned}}$

que suele expresarse como:

${\text{abs}}(x)=|x|=\left\{{\begin{array}{rcl}x,&{\mbox{si}}&x\geq 0\\-x,&{\mbox{si}}&x<0\end{array}}\right.$

Por definición, el valor absoluto de $x\,$ siempre será mayor o igual que cero y nunca negativo.

Esta función es continua en toda la recta real y es diferenciable en $\mathbb {R}$ menos en $x=0$.

Relación con la función signo

La función real valor absoluto de un número real devuelve su valor sin considerar el signo mientras que la función signo devuelve el signo de un número sin considerar su valor. Las siguientes ecuaciones muestran la relación entre estas dos funciones:

$|x|=x\operatorname {sgn} (x)$

o

$|x|\operatorname {sgn} (x)=x$

y para $x\neq 0$

$\operatorname {sgn} (x)={\frac {|x|}{x}}={\frac {x}{|x|}}$

Derivada

La función real valor absoluto tiene derivada para cada $x\neq 0$ pero no es diferenciable en $x=0$. Su derivada, para $x\neq 0$, está dada por la siguiente función

${\frac {d}{dx}}|x|={\frac {x}{|x|}}={\begin{cases}-1&x<0\\1&x>0\end{cases}}$

Para $x\neq 0$ la derivada de la función valor absoluto es la función signo

${\frac {d}{dx}}|x|=\operatorname {sgn} x$

Integral

La antiderivada (integral indefinida) de la función real valor absoluto es

$\int |x|dx={\frac {x|x|}{2}}+C$

donde $C$ es una constante de integración arbitraria.

Distancia

En general, el valor absoluto de la diferencia de dos números reales sirve para hallar la distancia entre ellos. De hecho, el concepto de función distancia o métrica en matemáticas se puede ver como una generalización del valor absoluto que expresa la distancia a lo largo de la recta numérica real.

• La función valor absoluto es una función continua en todo su dominio, con su función derivada discontinua esencial en (0;0), con dos ramas de valores constantes.
• La función y = x|x|, usando valor absoluto, es una función creciente y continua, su gráfica se obtiene de la gráfica de la parábola y=x², reflejando la rama izquierda respecto al eje Ox.

El conjunto de los reales con la norma definida por el valor absoluto $(\mathbb {R} ,|\cdot |)$ es un espacio de Banach.​

Valor absoluto de un número complejo

El valor absoluto de un número complejo $z\,$ es la distancia $r\,$ desde $z\,$ al origen. Aquí vemos que $z\,$ y su conjugado ${\bar {z}}\,$ tienen el mismo valor absoluto.

La generalización cabe. pues en R y C van a expresar la noción de distancia.

Como los números complejos no conforman un conjunto ordenado en el sentido de los reales, la generalización del concepto no es directa, sino que requiere de la siguiente identidad, que proporciona una definición alternativa y equivalente para el valor absoluto:

$|z|={\sqrt {zz^{*}}}$ donde z^* es el conjugado del número complejo z.

De esta manera, dado cualquier número complejo de la forma

$z=x+iy\,$

con x e y números reales, el valor absoluto o módulo de z está definido formalmente por:

$|z|={\sqrt {x^{2}+y^{2}}}$

Como los números complejos son una generalización de los números reales, es lógico que podamos representar a estos últimos también de esta forma:

$|x+i0|={\sqrt {x^{2}+0^{2}}}={\sqrt {x^{2}}}=|x|$

De modo similar a la interpretación geométrica del valor absoluto para los números reales, se desprende del Teorema de Pitágoras que el valor absoluto de un número complejo corresponde a la distancia en el plano complejo de ese número hasta el origen, y más en general, que el valor absoluto de la diferencia de dos números complejos es igual a la distancia entre ellos.

Propiedades

El valor absoluto de los complejos comparte todas las propiedades vistas anteriormente para los números reales. Además, si

$z=x+iy=r(\cos \phi +i\sin \phi ),\qquad {\bar {z}}=x-iy$

es el conjugado de z, entonces se verifica que:

$|z|=r\,$

$|z|=|{\bar {z}}|$

$|z|={\sqrt {z{\bar {z}}}}$

Esta última fórmula es la versión compleja de la primera identidad en los reales que mencionamos en esta sección.

Como los números reales positivos forman un subgrupo de los números complejos bajo el operador de multiplicación, podemos pensar en el valor absoluto como un endomorfismo del grupo multiplicativo de los números complejos.

Generalizaciones

Números hipercomplejos

Además de en los números complejos la función valor absoluto puede extenderse a números hipercomplejos como los cuaterniones o los octoniones. En estas álgebras sobre los números reales el valor absoluto de un número h se define como:

$|h|={\sqrt {h{\bar {h}}}}$

Donde ${\bar {h}}$ representa el hiperconjungado de h.

Espacios vectoriales

En espacios vectoriales que no son álgebras sobre los reales, los conceptos de módulo, norma y seminorma generalizan la noción de valor absoluto de los números reales.

Números p-ádicos

El teorema de Ostrowski demuestra que sobre el cuerpo de los números racionales $\mathbb {Q}$ sólo se pueden definir un cierto número de normas no triviales con las propiedades del valor absoluto. Además del valor absoluto ordinario, se pueden definir las normas p-ádicas $|\cdot |_{p}$, que son no-aquimedeanas y que tienen esencialmente las mismas propiedades definitorias del valor absoluto ordinario, pero da lugar a una estructura topológica totalmente diferente.

Programación del valor absoluto

En programación, la función matemática utilizada comúnmente para calcular el valor absoluto es abs(). Esta se utiliza en los lenguajes de programación Fortran, Matlab y GNU Octave (los cuales la soportan para números enteros, reales y complejos), y además en el Lenguaje C, donde también son válidas las funciones labs(), llabs(), fabs(), fabsf() y fabsl().

La codificación de la función valor absoluto para valores enteros es sencilla:

int abs (int i)
{
    if (i < 0)
        return -i;
    else
        return i;
}

Sin embargo, al tratar con coma flotantes la codificación se complica, pues se debe lidiar con la infinitud y valores NaN.^{[cita requerida]}

Con el lenguaje ensamblador es posible calcular el valor absoluto de un número utilizando sólo tres instrucciones. Por ejemplo, para un registro de 32 bits en una arquitectura x86, con la sintaxis de Intel:

cdq
xor eax, edx
sub eax, edx

cdq extiende el bit de signo de eax en edx. Si eax es no-negativa, entonces edx se convierte en cero, y las dos últimas instrucciones no tienen efecto, dejando eax sin cambios. Si eax es negativa, entonces edx se convierte en 0xFFFFFFFF, o -1. Las siguientes dos instrucciones se convierten en una inversión complemento a dos, dejando el valor absoluto del valor negativo en eax.

Véase también

• Norma vectorial

Referencias y notas

Bibliografía

• Nahin, Paul J.; An Imaginary Tale; Princeton University Press; (hardcover, 1998). ISBN 0-691-02795-1
• O'Connor, John J.; Robertson, Edmund F., «Jean Robert Argand» (en inglés), MacTutor History of Mathematics archive, Universidad de Saint Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Argand.html .
• Schechter, Eric; Handbook of Analysis and Its Foundations, pp 259-263, "Absolute Values", Academic Press (1997) ISBN 0-12-622760-8
• Weisstein, Eric W. «Absolute Value». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• value Valor absoluto en PlanetMath.

Enlaces externos

• Wikimedia Commons alberga una galería multimedia sobre Valor absoluto.

• Datos: Q120812
• Multimedia: Absolute value / Q120812