Polígono infinito oblicuo
En geometría, un polígono alabeado infinito o apeirógono oblicuo es un 2-politopo infinito con vértices que no son todos colineales. Los polígonos oblicuos en zig-zag infinitos son formas bidimensionales con vértices que se alternan entre dos líneas rectas paralelas. A su vez, los polígonos helicoidales infinitos son formas tridimensionales con sus vértices en la superficie de un cilindro.[1]
Existen polígonos regulares oblicuos infinitos en los polígonos de Petrie de los grupos de Coxeter afines e hiperbólicos. Se construyen mediante un solo operador como el compuesto de todas las reflexiones del grupo de Coxeter.
Apeirógonos oblicuos en zig-zag regulares en dos dimensiones[editar]

Un apeirógono oblicuo en zig-zag regular tiene configuración (2*∞), con simetría de friso D∞d.
También se pueden identificar como los polígonos de Petrie de los tres mosaicos regulares del plano: {4,4}, {6,3} y {3,6}. Estos apeirógonos oblicuos en zig-zag regulares tienen polígonos regulares dentro de los mosaicos con ángulos interiores de 90°, 120° y 60° respectivamente:

|
Apeirógonos oblicuos isotoxales en dos dimensiones[editar]
Un apeirógono isotoxal tiene un tipo de aristas situadas entre dos tipos de vértices alternos. Posee un grado de libertad en el ángulo interior, α. {∞α} es el polígono dual de un apeirógono oblicuo isogonal.
| {∞0°} | |
| {∞30°} | 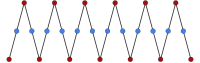
|
Apeirógonos oblicuos isogonales en dos dimensiones[editar]
Apeirógonos oblicuos en zig-zag isogonales en dos dimensiones[editar]
Un apeirógono sesgado isogonal alterna dos tipos de aristas con varias simetrías de friso. Los apeirógons oblicuos en zig-zag regulares distorsionados producen apeirógonos oblicuos en zig-zag isogonales con simetría traslacional:
| p1, [∞]+, (∞∞), C∞ | |
|---|---|
 
|
 
|
Apeirógonos oblicuos alargados isogonales en dos dimensiones[editar]
Otros apeirógonos oblicuos isogonales tienen aristas alternas paralelas a la dirección del friso. Estos apeirógonos oblicuos alargados isogonales tienen simetría de espejo vertical en los puntos medios de los bordes paralelos a la dirección del friso:
| p2mg, [2+,∞], (2*∞), D∞d | ||
|---|---|---|
 |
||
Apeirógonos oblicuos alargados cuasiregulares en dos dimensiones[editar]
Un apeirógono oblicuo alargado isogonal tiene dos tipos de aristas diferentes; si sus dos tipos de arista tienen la misma longitud: no puede llamarse regular porque sus dos tipos de arista siguen siendo diferentes ("trans-borde" y "cis-borde"), pero puede llamarse cuasiregular.
Los apeirógonos oblicuos alargados cuasiregulares de ejemplo se pueden ver como polígonos de Petrie truncados en mosaicos regulares truncados del plano euclídeo:
Apeirógonos oblicuos hiperbólicos[editar]
Los polígonos oblicuos regulares infinitos se encuentran de manera similar en el plano euclídeo y en el plano hiperbólico.
Los polígonos oblicuos regulares infinitos hiperbólicos también existen como caminos de aristas en zigzag de polígonos de Petrie en todos los teselados regulares del plano hiperbólico. Y nuevamente, como en el plano euclídeo, los polígonos oblicuos cuasiregulares infinitos hiperbólicos se pueden construir como polígonos de Petrie truncados dentro de las aristas de todos los mosaicos regulares truncados del plano hiperbólico.
| {3,7} | t{3,7} |
|---|---|
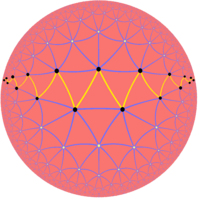 Oblicuo regular |
 Oblicuo cuasiregular |
Polígonos helicoidales infinitos en tres dimensiones[editar]
{∞} # {3} Un polígono helicoidal regular infinito (visto en perspectiva) |
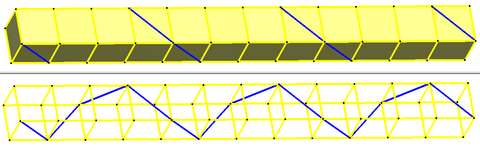
Un polígono infinito helicoidal (oblicuo) puede existir en tres dimensiones, donde los vértices pueden verse como limitados a la superficie de un cilindro. El boceto de la derecha es una vista en perspectiva 3D de un polígono helicoidal regular infinito.
Este polígono helicoidal infinito se puede ver principalmente como construido a partir de los vértices en una pila infinita de prismas o antiprismas n-gonales uniformes, aunque en general el ángulo de torsión no se limita a un divisor entero de 180°. Un polígono helicoidal infinito (oblicuo) tiene simetría respecto al eje helicoidal.
Una pila infinita de prismas, por ejemplo cubos, contiene un polígono helicoidal infinito en las diagonales de las caras cuadradas, con un ángulo de giro de 90° y con un símbolo de Schläfli {∞} # {4}.
Una pila infinita de antiprismas, por ejemplo octaedros, forma polígonos helicoidales infinitos, resaltados aquí en rojo, verde y azul, cada uno con un ángulo de giro de 60° y con un símbolo de Schläfli {∞} # {6} .
Archivo:Octahedron stack helix apeirógonos.png
Una secuencia de aristas de una hélice de Boerdijk-Coxeter puede representar infinitos polígonos helicoidales regulares con un ángulo de torsión irracional:
Polígonos helicoidales isogonales infinitos en tres dimensiones[editar]
Una pila de prismas rectos puede generar apeirógonos helicoidales isogonales que alternan aristas alrededor del eje y en el eje; por ejemplo, una pila de cubos puede generar este apeirógono helicoidal isogonal alternando aristas rojas y azules:
De manera similar, una pila alterna de prismas y antiprismas puede producir un polígono helicoidal isogonal infinito, como por ejemplo, una pila de prismas y antiprismas triangulares con un polígono helicoidal isogonal infinito:
También se puede construir un polígono helicoidal isogonal infinito con un ángulo de giro irracional a partir de tetraedros truncados apilados como una hélice de Boerdijk-Coxeter, alternando dos tipos de aristas, entre pares de caras hexagonales y pares de caras triangulares:
Referencias[editar]
- ↑ The Coxeter Legacy: Reflections and Projections. American Mathematical Soc. pp. 108 de 320. ISBN 9780821887608. Consultado el 6 de julio de 2022.
Bibliografía[editar]
- Coxeter, H.S.M.; Regular complex polytopes (1974). Chapter 1. Regular polygons, 1.5. Regular polygons in n dimensions, 1.7. Zigzag and antiprismatic polygons, 1.8. Helical polygons. 4.3. Flags and Orthoschemes, 11.3. Petrie polygons