Usuario:Pololita2112/Taller

ESPACIO EUCLIDIANO EN DOS DIMENSIONES

INTRODUCCION

El espacio euclidiano bidimensional o simplemente espacio bidimensional (también conocido como espacio 2D , 2 espacios o plano euclidiano ) es un entorno geométrico en el que se requieren dos valores (llamados parámetros) para determinar la posición de un elemento (es decir, punto ) en el plano . Es la versión bidimensional del espacio euclidiano .El conjunto estilo de visualización de pares de números reales (espacio de coordenadas reales) con la estructura adecuada a menudo sirve como ejemplo canónico.​

Curvatura mínima de superficie

​

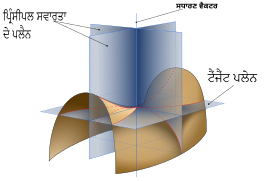
El plano en esta época se describe como un sistema de coordenadas cartesianas, que especifica cada punto de forma única en un plano mediante un par de coordenadas numéricas , que son las distancias con signo desde el punto a dos líneas fijas perpendiculares dirigidas, medidas en la misma unidad de longitud . Cada línea de referencia se denomina eje de coordenadas o simplemente eje del sistema, y el punto donde se encuentran es su origen , generalmente en un par ordenado (0,0). Las coordenadas también se pueden definir como las posiciones de los Proyecciones perpendiculares del punto sobre los dos ejes, expresadas como distancias con signo desde el origen.​

La idea de este sistema fue desarrollada en 1637 en escritos de Descartes y de forma independiente por Pierre de Fermat, aunque Fermat también trabajó en tres dimensiones, y no publicó el descubrimiento. Ambos autores usaron un solo eje en sus tratamientos y tienen una longitud variable medida en referencia a este eje. El concepto de utilizar un par de hachas se introdujo más tarde, después de que la Geometría de Descartes fuera traducida al latín en 1649 por Frans van Schooten y sus alumnos.

Más tarde, se pensó en el plano como un campo , donde dos puntos cualesquiera podían multiplicarse y, excepto 0, dividirse. Esto se conocía como el plano complejo . El plano complejo a veces se denomina plano de Argand porque se utiliza en los diagramas de Argand. Estos llevan el nombre de Jean-Robert Argand (1768–1822), aunque fueron descritos por primera vez por el agrimensor y matemático danés-noruego Caspar Wessel (1745–1818).  Los diagramas de Argand se utilizan con frecuencia para trazar las posiciones de los polos y ceros de una función en el plano complejo.​

SISTEMA DE COORDENADAS EN EL PLANO

Sistema de coordenadas cartesianas

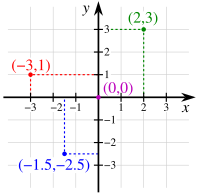
En matemáticas, la geometría analítica (también llamada geometría cartesiana) describe cada punto en un espacio bidimensional por medio de dos coordenadas. Se dan dos ejes de coordenadas perpendiculares que se cruzan en el origen . Por lo general, están etiquetados como x e y . En relación con estos ejes, la posición de cualquier punto en el espacio bidimensional viene dada por un par ordenado de números reales, cada número da la distancia de ese punto desde el origen medida a lo largo del eje dado, que es igual a la distancia de ese punto. punto del otro eje.

Otro sistema de coordenadas ampliamente utilizado es el sistema de coordenadas polares, que especifica un punto en términos de su distancia desde el origen y su ángulo relativo a un rayo de referencia hacia la derecha.​

ALGEBRA LINEAL

Otra forma matemática de ver el espacio bidimensional se encuentra en el álgebra lineal, donde la idea de independencia es crucial. El plano tiene dos dimensiones porque la longitud de un rectángulo es independiente de su ancho. En el lenguaje técnico del álgebra lineal, el plano es bidimensional porque cada punto del plano puede describirse mediante una combinación lineal de dos vectores independientes .​Para llegar a ello se debe tener en cuenta el producto punto o producto escalar de dos vectores es una operación que da como resultado un número real. Hay distintas formas de definir esta operación, una de ellas es por medio de multiplicar el producto de los módulos de los vectores por el coseno del ángulo que forman, esto es : A = [ A ₁ , A ₂ ] y B = [ B ₁ , B ₂ ] ​, y por defecto, su magnitud ángulo y longitud.

MAGNITUD, ANGULO Y LONGITUD

Coordenadas polares

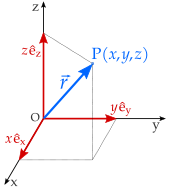
Como cualquier punto en el plano se puede escribir en la forma (x, y), es evidente que se puede pensar que cualquier punto en el plano es un vector en R2, y viceversa. De este modo, los términos “el plano” y “R2” con frecuencia son intercambiables. Sin embargo, para muchas aplicaciones físicas (incluyendo las nociones de fuerza, velocidad, aceleración y momento) es importante pensar en un vector no como un punto sino como una entidad que tiene “longitud” y “dirección”. Ahora se verá cómo se lleva a cabo esto. Un vector se puede representar como una flecha. Puesto que en realidad un vector es un conjunto de segmentos de recta equivalentes, se define la magnitud o longitud de un vector como la longitud de cualquiera de sus representaciones y su dirección como la dirección de cualquiera de sus representaciones. Haciendo uso de la representación 0SR y escribiendo el vector v 5 (a, b) se define que su magnitud es su longitud, y su dirección es la que señala la flecha. En este orden de ideas, el producto escalar de dos vectores euclidianos A y B se define por donde θ es el ángulo entre A y B ​

PRODUCTO PUNTO

En álgebra lineal el producto vectorial, mejor conocido como producto cruz es una aplicación cuyo dominio es V² y su codominio es K, donde V es un espacio vectorial y K el conjunto de los escalares respectivos. Esta aplicación amplia la oportunidad de emplear los conceptos de la geometría Euclidiana tradicional: longitudes, ángulos y ortogonalidad en 2 y 3 dimensiones.

EN TOPOLOGIA

En Topología el plano es considerado como un espacio topológico en dos dimensiones.

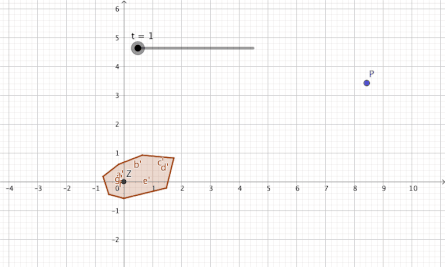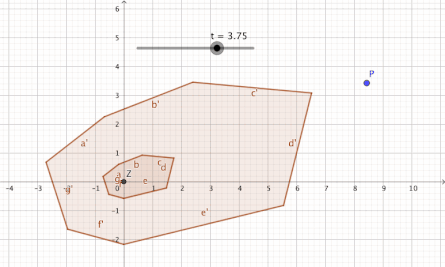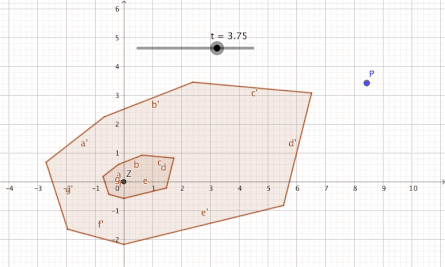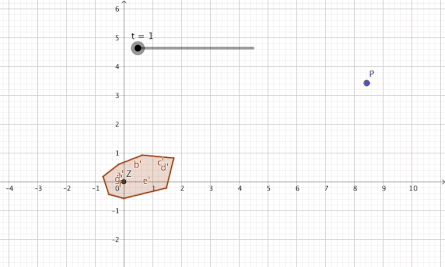
Esta dimensión se caracteriza por el hecho de que removiendo un punto del plano deja un espacio que está conectado, pero no simplemente conectado.

ACERCA DEL ESPACIO EUCLIDIANO

Además de su conocida estructura geométrica, con isomorfismos que son isometrías con respecto al producto interior habitual, el plano puede considerarse en otros niveles de abstracción. Cada nivel de abstracción corresponde a una categoría específica.

En un extremo, todos los conceptos geométricos y métricos pueden abandonarse para dejar el plano topológico, que puede considerarse como una hoja de goma infinita idealizada homotópicamente trivial, que conserva la noción de proximidad, pero no tiene distancias. El plano topológico tiene el concepto de trayectoria lineal, pero no el de línea recta. El plano topológico, o su equivalente el disco abierto, es la vecindad topológica básica utilizada para construir superficies (o 2manifolds) clasificadas en topología de baja dimensión. Los isomorfismos del plano topológico son todos biyecciones continuas. El plano topológico es el contexto natural de la rama de la teoría de grafos que se ocupa de los grafos planos y de resultados como el teorema de los cuatro colores.

ACERCA DE LA GEOMETRÍA DIFERENCIAL

La geometría diferencial considera el plano como un colector real de dos dimensiones, un plano topológico dotado de una estructura diferencial. De nuevo en este caso, no existe la noción de distancia, pero ahora hay un concepto de suavidad de los mapas, por ejemplo un camino diferenciable o suave (dependiendo del tipo de estructura diferencial aplicada). Los isomorfismos en este caso son biyecciones con el grado de diferenciabilidad elegido.

NOCIONES DE TOPOLOGIA Y GEOMETRIA DIFEFENCIAL

ESFERA DE RIEMMAN

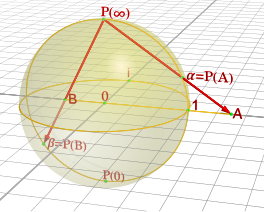
La compactación de un punto del plano es homeomorfa a una esfera (véase la proyección estereográfica); el disco abierto es homeomorfo a una esfera a la que le falta el "polo norte"; añadiendo ese punto se completa la esfera (compacta). El resultado de esta compactación es un colector denominado esfera de Riemann o línea proyectiva compleja. La proyección del plano euclidiano a una esfera sin punto es un difeomorfismo e incluso un mapa conforme.

El propio plano es homeomorfo (y difeomorfo) a un disco abierto. Para el plano hiperbólico dicho difeomorfismo es conforme, pero para el plano euclidiano no lo es.

Mientras que la topología diferencial se centra únicamente en las propiedades topológicas de las variedades, la geometría diferencial permite aplicar resultados conocidos del cálculo multivariable a las aplicaciones entre variedades. Está bien definida cuando las imágenes de ambas cartas tienen intersección no vacía. Estas funciones se denominan funciones de transición, y son funciones reales de varias variables, cuyas propiedades son bien conocidas. Dependiendo de qué propiedades tengan estas funciones, se hablara de un tipo de variedad o de otra.