Poliedro de Waterman

En geometría, los poliedros de Waterman son una familia de poliedros descubierta alrededor de 1990 por el matemático Steve Waterman. Un poliedro de Waterman se crea a partir de empaquetamientos de esferas de acuerdo con una disposición cúbica compacta (DCC), también conocida como empaquetado cúbico centrado en caras (ccc), eliminando las esferas cuyo centro queda más lejos que un radio definido,^[1] y a continuación creando la envolvente convexa de los centros de las esferas restantes.

Los poliedros de Waterman forman una vasta familia de poliedros. Algunos de ellos tienen una serie de propiedades usuales, como múltiples simetrías o formas interesantes y regulares. Otros son solo una colección de caras irregulares formadas a partir de polígonos convexos.

Los poliedros de Waterman más populares son aquellos con centros en el punto (0,0,0) y construidos a partir de cientos de polígonos. Tales poliedros se asemejan a esferas. De hecho, cuantas más caras tiene un poliedro de Waterman, más se parece a su esfera circunscrita en volumen y área total.

Con cada punto del espacio 3D se puede asociar una familia de poliedros de Waterman con diferentes valores de radios de las esferas circunscritas. Por tanto, desde un punto de vista matemático se pueden considerar los poliedros de Waterman como espacios 4D W (x, y, z, r), donde x, y, z son coordenadas de un punto en 3D, y r (el radio de corte) es un número positivo mayor que 1.^[2]

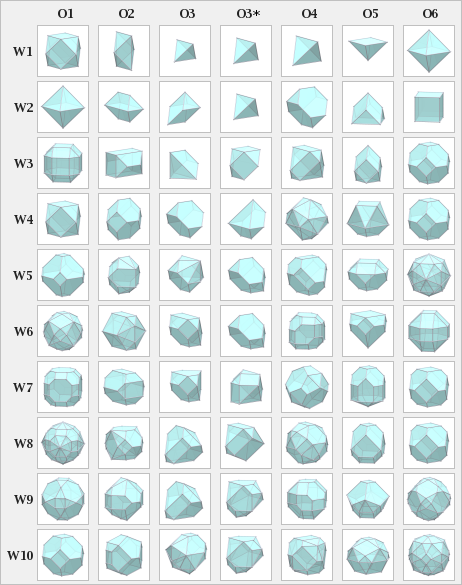
Siete orígenes de la disposición cúbico compacta (st) (DCC)[editar]

Puede haber siete orígenes definidos en una disposición cúbica compacta de esferas (DCC),^[3] donde n = {1, 2, 3,…}:

Origen 1: desplazamiento 0,0,0, radio ${\sqrt {2n}}$
Origen 2: desplazamiento 1/2, 1/2, 0, radio ${\tfrac {1}{2}}{\sqrt {2+4n}}$
Origen 3: desplazamiento 1/3, 1/3, 2/3, radio ${\tfrac {1}{3}}{\sqrt {6(n+1)}}$
Origen 3*: desplazamiento 1/3, 1/3, 1/3, radio ${\tfrac {1}{3}}{\sqrt {3+6n}}$
Origen 4: desplazamiento 1/2, 1/2, 1/2, radio ${\tfrac {1}{2}}{\sqrt {3+8(n-1)}}$
Origen 5: desplazamiento 0,0, 1/2, radio ${\tfrac {1}{2}}{\sqrt {1+4n}}$
Origen 6: desplazamiento 1,0,0, radio ${\sqrt {1+2(n-1)}}$

Dependiendo del origen del barrido se obtiene una forma diferente, a la que se asocia un poliedro resultante.

Relación con los sólidos platónicos y de Arquímedes[editar]

Algunos poliedros de Waterman crean sólidos platónicos y sólidos arquimedianos. Para establecer esta relación con mayor facilidad, es conveniente normalizar los poliedros de Waterman. Por ejemplo, W2 O1 tiene un tamaño y volumen diferentes que W1 O6, pero tiene la misma forma que un octaedro.

Sólidos platónicos[editar]

Tetraedro: W1 O3 *, W2 O3 *, W1 O3, W1 O4
Octaedro: W2 O1, W1 O6
Cubo: W2 O6
El icosaedro y el dodecaedro no tienen representación como poliedros de Waterman.

Sólidos de Arquímedes[editar]

Cuboctaedro: W1 O1, W4 O1
Octaedro truncado: W10 O1
Tetraedro truncado: W4 O3, W2 O4
Los otros sólidos de Arquímedes no tienen representación como poliedros de Waterman.

El W7 O1 podría confundirse con un cuboctaedro truncado, y W3 O1 = W12 O1 podría confundirse con un rombicuboctaedro, pero esos poliedros de Waterman tienen dos longitudes de arista y, por lo tanto, no se clasifican como sólidos de Arquímedes.

Poliedros de Waterman generalizados[editar]

Los poliedros de Waterman generalizados se definen como el recubrimiento convexo derivado del conjunto de puntos de cualquier extracción esférica de una celosía regular.

Se incluye un análisis detallado de las siguientes 10 celosías: bcc, cuboctaedro, diamante, fcc, hcp, octaedro truncado, rombododecaedro, cúbico simple, tet tet truncado, tet truncado cuboctaedro octaedro truncado.

Cada una de las 10 celosías se examinó para aislar esos puntos de origen particulares que manifestaban un poliedro único, además de poseer algún requisito mínimo de simetría. Desde un punto de origen viable, dentro de una red, existe una serie ilimitada de poliedros. Dado un intervalo de barrido adecuado, existe una correspondencia uno a uno entre cada conjunto de números enteros y un poliedro de Waterman generalizado.