Teoría de vigas de Timoshenko

La teoría de vigas de Timoshenko fue desarrollada por el ingeniero ucraniano-estadounidense Stephen Timoshenko, estableciéndose como un modelo matemático riguroso ampliamente utilizado para describir la vibración transversal de vigas, postulado en la década de 1920. También denominada la teoría de vigas gruesas. Históricamente el primer modelo de viga importante fue la Teoría de Vigas de Euler-Bernoulli o teoría clásica de vigas como consecuencia de las obras de Bernoulli (Jacob y Daniel) y Euler, creado en el año de 1744. En 1921 y 1922, Timoshenko propuso una mejora al añadir el efecto de deformación de corte. Mostró, a través del ejemplo de una viga apoyada sencilla, que la corrección frente a cortante es cuatro veces más importante debido a la inercia de rotación en comparación con la teoría de Euler-Bernoulli.[1]
Suposiciones básicas[editar]
Las suposiciones básicas de la teoría de vigas de Timoshenko están dadas por.
- El material del elemento es homogéneo, isotrópico y lineal elástico; cumpliendo la ley de elasticidad de Hooke. Coeficiente de Poisson despreciable.
- El desplazamiento vertical de los puntos que se encuentran sobre la sección transversal del elemento en una posición , son pequeños e iguales a los desplazamientos del eje de la viga.
- El desplazamiento lateral a lo largo del eje de la viga es nulo.
- La sección transversal del elemento en una posición normal al eje de la viga antes de la deformación, permanece plana pero no necesariamente ortogonal al eje del elemento después de la deformación. Esto supone la presencia de un estado de tensiones cortantes en la sección de la viga ().
Esta última suposición es la principal diferencia entre la teoría de vigas de Euler-Bernoulli y Timoshenko, que representa una mejor aproximación de la deformación de la sección transversal en vigas de gran peralte.
Campo de Desplazamientos[editar]
Teniendo en cuenta las suposiciones anteriores podemos definir el campo de desplazamientos. Así, por suposición número tres tenemos que:
En donde representa la pendiente del eje de la viga y representa una rotación adicional debida a la distorsión de la sección transversal. Por lo tanto,
Campo de Deformaciones[editar]
A partir del campo de desplazamientos, las relaciones deformación-desplazamiento para el caso de deformaciones infinitesimales proporcionan las deformaciones normales y angulares del siguiente modo:
Deformaciones normales:
Deformaciones angulares:
Se observa que la hipótesis cinemática principal de la Teoría de Vigas de Timoshenko (suposición básica n°4) introduce una deformación angular , que expresada en valor absoluto es igual a la rotación y que, dado que es independiente de las coordenadas , está uniformemente distribuida en la sección transversal de la viga. Esta es la principal diferencia con la teoría de vigas de Euler-Bernoulli, cuyas hipótesis cinemáticas conducen a . Como se verá más adelante, en virtud de las ecuaciones de Lamé para el esfuerzo cortante, la presencia de la deformación angular en la teoría de Timoshenko supone la existencia de tensiones tangenciales a la sección transversal de la viga, uniformemente distribuidas en ella.
Campo de Esfuerzos[editar]
Teniendo en cuenta que esta teoría supone el Coeficiente de Poisson es despreciable para el cálculo de los esfuerzos normales pero no para los esfuerzos tangenciales, podemos expresar el campo de esfuerzos con la ayuda de las ecuaciones de Lamé como sigue:
Y que los esfuerzos tangenciales se escriben como:
En donde tenemos que es el Módulo de Young, es el Módulo Cortante o Módulo de Cizalladura, es uno de los Parámetros de Lamé y es la dilatación cúbica, que se calcula como .
Fuerzas Internas (momento flector y fuerza cortante)[editar]
Podemos definir el momento flector actuante sobre el elemento, como la sumatoria de una par de fuerzas que actúan sobre la sección transversal, representadas por los esfuerzos normales actuando sobre el área de la sección transversal de la viga. Podemos expresar esto matemáticamente como:
Del mismo modo podemos definir la fuerza cortante actuante en la viga, como la sumatoria de las fuerzas actuantes sobre la sección transversal de la viga, es decir, los esfuerzos cortantes que actúan sobre el área de la sección transversal del elemento. Matemáticamente se expresa como:
Reemplazando en estas expresiones el valor de los esfuerzos normales () y los esfuerzos cortantes () obtenidos en el apartado anterior, tenemos que:
En donde es la deformación por flexión del elemento. Es de interés apreciar que y dependen únicamente del eje coordenado .
La expresión para los esfuerzos normales (), nos indica que la variación a través del espesor del elemento es lineal, la cual podemos considerar exacta, de acuerdo con la teoría clásica de vigas.[2] En contraparte, la expresión para los esfuerzos tangenciales (), nos muestra que su distribución en la sección transversal es uniforme (independiente de las coordenadas y ). Este resultado puede considerarse como una "mejora" en comparación con la teoría de Euler-Bernoulli, que predice y incluso si la fuerza cortante es no nula.
Aun así, el resultado de la teoría de Timoshenko de uniformemente distribuido en la sección transversal tampoco puede considerarse como exacto, ya que está en clara contradicción, por ejemplo, con la distribución parabólica de presente en los elementos de sección rectangular[2] que se deduce en forma exacta utilizando la fórmula de Collignon. Con el fin de contrarrestar este problema, se adopta un coeficiente de forma o distorsión , que busca hacer coincidir el trabajo de deformación constante con el exacto. De este modo podemos expresar el esfuerzo tangencial () y la fuerza cortante como:
Donde se denomina área reducida de la sección transversal. El coeficiente de forma depende de la forma de la sección transversal y del coeficiente de Poisson y está en el rango . La determinación precisa de este coeficiente no es sencilla en el caso general y varios autores han proporcionado estimaciones para distintas secciones transversales; por ejemplo, Cowper (1966)[3] proporcionó expresiones para para secciones de tipo rectangular, circular y tubo de pared delgada, entre otras.
La tabla siguiente muestra el factor de corrección de cortante para vigas con materiales elásticos isotrópicos, según Cowper, para las secciones más comunes.
| sección transversal | coeficiente |
|---|---|

|
|

|
|

|
|

|
, donde |

|
|

|
|

|
, donde y |
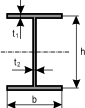
|
, donde y |
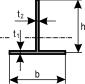
|
, donde y |
donde es el coeficiente de Poisson.
Deformada de la viga en el caso cuasiestático[editar]

Interesa a continuación encontrar el campo de desplazamientos transversales , que nos da la forma de la viga deformada en términos de las acciones externas, que pueden ser fuerzas perpendiculares al eje de la viga (puntuales o distribuidas), así como pares concentrados. Eventualmente, podría ser necesario también obtener el giro de la sección transversal . Comenzaremos planteando las ecuaciones de equilibrio para un elemento diferencial de viga como el que se muestra en la figura, en la que además se explicita la convención de signos que se utilizará en este desarrollo.
Del equilibrio de fuerzas en dirección para el elemento diferencial, se obtiene:
Del equilibrio de momentos, se obtiene:
Por otra parte, combinando la expresión para el momento flector obtenida en el apartado anterior, con la expresión para proporcionada más arriba (en el apartado sobre Campo de Desplazamientos) y utilizando , se obtiene:
- donde, de lo visto en el apartado anterior,
Alternativa 1
Si se combina las dos expresiones anteriores y se considera, además, el equilibrio de fuerzas verticales, se obtiene una ecuación diferencial de segundo orden en incógnita , que puede resolverse por doble integración si se conoce dos condiciones de contorno y si se conoce la distribución del momento flector . (Se observa que la fuerza distribuida usualmente es un dato del problema). Esta ecuación es:
Alternativa 2
Si se deriva con respecto a la ecuación de equilibrio de momentos y se considera la relación obtenida en el apartado sobre Fuerzas Internas, se obtiene:
- donde :
Si se combina estas dos expresiones considerando nuevamente la relación entre y el cortante y asumiendo sección transversal constante, se obtiene una ecuación diferencial en la que aparece la derivada de la fuerza cortante con respecto a . Esta derivada se puede eliminar usando el equilibrio de fuerzas expresado más arriba, para obtener una ecuación diferencial de cuarto orden en incógnita que podrá resolverse en términos de la carga distribuida , siempre que se conozca cuatro condiciones de contorno. Esta ecuación es:
Alternativa 3
En forma alternativa, es posible encontrar la deformada de la viga resolviendo en forma escalonada dos ecuaciones diferenciales de primer orden: la primera de ellas es simplemente la relación ya mencionada, mientras que la segunda proviene de reescribir la expresión para dada en el apartado sobre Campo de Desplazamientos, teniendo en consideración (1), la relación ; (2), la relación entre y el cortante y (3), la ecuación de equilibrio de momentos. Las dos ecuaciones diferenciales mencionadas son las siguientes:
La primera ecuación puede resolverse para en términos del momento flector si se conoce una condición de contorno para el giro de la sección transversal de la viga. Una vez hallado podrá resolverse la segunda ecuación para en términos del cortante si se conoce una condición de contorno para la deformada.
Bibliografía[editar]
- Oñate, Eugenio (2013). «2». Structural Analysis with the Finite Element Method Linear Statics Volume 2. Beams, Plates and Shells (en inglés). Springer. p. 864.
- Magrab, Edward B. (2012). «5». Vibrations of Elastic Systems With Applications to MEMS and NEMS (en inglés). Springer. p. 489.
Referencias[editar]
- ↑ Loudini, Malik. [Malik Loudini (2010). Timoshenko Beam Theory based Dynamic Modeling of Lightweight Flexible Link Robotic Manipulators, Advances in Robot Manipulators, Ernest Hall (Ed.), ISBN 978-953-307-070-4, InTech, DOI: 10.5772/9661. Available from: http://www.intechopen.com/books/advances-in-robot-manipulators/timoshenko-beam-theory-based-dynamic-modeling-of-lightweight-flexible-link-robotic-manipulators «Timoshenko Beam Theory based Dynamic Modeling of Lightweight Flexible Link Robotic Manipulators»].
- ↑ a b Timoshenko, S.P. «Strength of Materials. Part 1: Elementary Theory and Problems».
- ↑ Cowper, G.R. (1966). «The Shear Coefficient in Timoshenko’s Beam Theory». Journal of Applied Mechanics 33 (2): 335-340. doi:10.1115/1.3625046.






































































