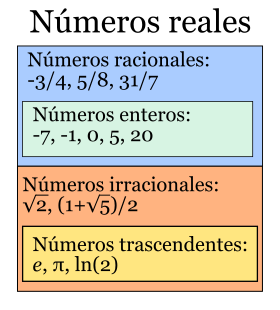
Clasificación de los números Reales[editar]

El sistema de los números reales consiste de un conjunto de elementos denominados números que dan sentido a las operaciones fundamentales conocidas como suma, resta, multiplicación, división, resolución de ecuaciones y proceso algebraicos.

Generalmente la mayoría de los textos de matemáticas representan los números reales con el símbolo R.

Propiedades de los números reales[editar]

Los números reales en general sirven para contar elementos de conjuntos de ese tipo de objetos. Sin embargo, los números tienen una cualidad aun más importante, que es aquella de medir cantidades Físicas, longitudes, áreas, volúmenes, etc.

Las operaciones del cálculo se sustentan en el sistema de los números reales y en sus propiedades.

Propiedad transitiva de la igualdad. Si a=b y b=c entonces a=c. Por ejemplo, si Sí 3 = 3 y 3 = 3 → = 3.

Propiedad conmutativa de la suma y de la multiplicación.

a + b = b + a y a . b = b

Propiedad asociativa de la suma y multiplicación.

a + (b + c) = (a + b) + c y a (b . c ) = ( a . b) c.

Propiedad del inverso: para cada número real a, existe un único número real denotado por - a, tal que: a + ( -a) = 0, el número -a es llamado inverso aditivo de a.

Propiedad distributiva:

a (b +c) = ab + ac.

Un numero real puede ser positivo, negativo o cero e identificarse por clases de números Los hay de dos clases, racionales e irracionales.

Definición de desigualdad[editar]

Dos expresiones relacionadas mediante los signos <, ≤ (menor igual), >, ≥ (mayor igual), o bien el signo ≠(diferente de) forman una desigualdad o inecuación, puesto que en las ecuaciones solamente se hace uso del símbolo de igualdad =

Propiedades de las desigualdades[editar]

Si a > b, entonces b < a. Ejemplo 5 > 3, entonces 3 < 5. Del mismo modo, si a > b y b >c, entonces a >c. Ejemplo 5 >3 y 3 >2, entonces 5 >2.

Las desigualdades anteriores se pueden unir en forma anidada como a: a >b >c, o bien a < b < c.

Si a > b y n es un número real cualquiera, entonces es válida la operación: a + n > b + n. Lo cual significa que ambos miembros de la desigualdad se les puede sumar o restar un número y como resultado se obtendrá una desigualdad en el mismo sentido. Ejemplo 5 > -1, si sumamos en ambos lados el número n = 3, tendremos 5 + 3 > -1 + 3, ósea, 8 >2.

Si a > b y n en un número positivo: an >bn, lo cual significa que el sentido de la desigualdad no se altera. Al multiplicar ambos miembros de una desigualdad por un número negativo n<0 el sentido de la desigualdad cambiará, es decir, si a > b y n < 0, se tiene que an <bn.

 Ejemplo 5 >1 al multiplicar por -5, obtenemos -25 <5, lo cual es verdadero. Pruébese con un ejemplo que lo mismo ocurre al dividir una desigualdad por n <0.

Suma de desigualdades. Dos desigualdades en un mismo sentido se pueden sumar miembro a miembro de manera que se obtenga una desigualdad en el mismo sentido: Si

  a >b y c >d entonces a + c >b + d. Ejemplo, si 4 >2 y 0 > -1 entonces 4 + 0 > 2 + ( -1), o bien 4 > 2. El ejemplo pone en evidencia la resta de desigualdades en el mismo sentido.

Resta de desigualdades. Dos desigualdades en sentido contrario se pueden restar miembro a miembro, dando por resultado una desigualdad del mismo sentido que la primera de las desigualdades. Si a>b y c <d, y de la primera restamos la segunda, a – c >b -d, y de la primera restamos la segunda, a -c >b -d. Ejemplo, 7 >1 y 2 < 5, obtenemos 7 – 2 >1 – 5, o sea: 5 > -4.

Multiplicación de desigualdades. Dos desigualdades de igual sentido se pueden multiplicar entre sí miembro a miembro si todos sus miembros son positivos, dando por resultado una desigualdad del mismo sentido. Si a <b y c < d (siendo a >o y c >o) entonces ac <bd. Ejemplo 3 < 5 y 8 <10, luego 3 (8) <5 (10), es decir: 24 <50.

División de desigualdades. Dos desigualdades de sentido contrario se pueden dividir miembro a miembro si todos los miembros de la desigualdad son números positivos, como resultado se obtendrá una desigualdad en el sentido de la primera de ellas. Si a >b y c < d

 (con b > 0 y c > 0) Ejemplo. 5 >1 y 2 <7.

Clasificación de las desigualdades[editar]

Desigualdad Lineales.

Son las más sencillas puesto que solamente contienen la variable a la primera potencia.

Desigualdades lineales dobles:

Son desigualdades lineales que contienen dos signos de comparación.

Desigualdades cuadráticas:

Como su nombre lo indica son aquellas en las que uno de sus miembros o en ambos aparece el termino cuadrático.

Desigualdades racionales:

Son aquellas en las que aparece cocientes con variable en el denominador y7o numerador.

Qué es una función y cuales son sus propiedades[editar]

Qué es una función. Cuando dos cantidades están ligadas de tal manera, que dándose el valor de una de ellas, se pueda determinar el valor correspondiente de la otra, se dice que cada una de las variables es función de la otra.

Propiedades de la función.

Elemento de lista de viñetas
Continuidad.
Monotonía.
Simetría.
Periodicidad.

Las funciones elementales básicas y las propiedades particulares de cada una[editar]

Continuidad.[editar]

Si una función y=f(x) pude representarse en todo su dominio mediante un trazo continuo decimos que dicha función es continua. Es decir, si puedes dibujar la gráfica de la función sin levantar el lápiz dicha función es continua.

En cambio, cuando tenemos que levantar el lápiz para trazar la gráfica de la función, se dice que es discontinua. Puede ocurrir que una función sea discontinua en su dominio para determinados puntos.

Monotonía.[editar]

Lo mismo podemos decir en una función: un tramo de función en el que según avanzamos a lo largo del eje X la gráfica sube es un tramo donde la función es creciente y un tramo de función en el que según avanzamos a lo largo del eje X la gráfica baja es un tramo donde la función es decreciente.

Los tramos de crecimiento y decrecimiento de una función los expresamos siempre mediante intervalos del eje X abiertos, es decir, expresas entre dónde y dónde (del eje X) crece la función. Los máximos y los mínimos los indicamos con sus coordenadas.

Simetría.[editar]

Gráficamente es muy fácil de observar la simetría. Matemáticamente lo que tenemos es que f(x)=f(-x). Es decir, que a la abscisa x>0 le va a corresponder la misma ordenada (o y) que a la abscisa x<0.

Podemos encontrar también la denominada simetría respecto al origen. En este caso tenemos que f(x)=-f(-x). Gráficamente se observa que es como si la función se reflejara en la recta que divide en dos partes iguales a los cuadrantes 2 y 4, es decir, dicha recta es ahora el eje de simetría.

Matemáticamente lo que tenemos es que, por ejemplo, si para x=1 la ordenada es y=1, tendremos que para la abscisa opuesta (x=-1), la ordenada es la opuesta también (y=-1).

Periodicidad.[editar]

Recordemos que un fenómeno se dice que es periódico si siempre transcurre el mismo intervalo de tiempo entre la primera vez que el ocurre el fenómeno, la segunda vez que ocurre, la tercera…Ese intervalo de tiempo se denomina, como no, período.

Existen funciones que son periódicas, es decir, que sus valores se repiten siempre cada intervalo determinado del eje x. Ese intervalo es el período de la función.

Definición de variable[editar]

Una variable x es una cantidad medible que aumenta o disminuye.

La cualidad principal de la variable es que representan el movimiento de los fenómenos físicos y geométricos que se estudian a través del calculo diferencial. No obstante, las variables adoptan el movimiento desde diferentes contextos de la matemática; anotemos los siguientes:

a) Aritmético: Se conciben como números reales contenidos en la recta real. Por ejemplo, en un segmento de recta, la variable x se mueve en el intervalo (a, b) tomando una cantidad inconmensurable de valores. La variación de x en el intervalo (a, b) es supuesto por la cantidad de valores que es susceptible de tomar.

b) Geométrico: las variables, como x, se asignan a las cantidades que cambian o adquieren movimiento en las figuras geométricas. Las figuras sueles ser puntos, distancias, áreas, ángulos, radianes, volúmenes, etc. Otra característica importante es que las magnitudes geométricas como las citadas, pueden idealizar cantidades físicas reales. Por ejemplo, las longitudes en el diseño de una caja, el vuelo de un avión, etc.

c) Las variables pueden representar entidades físicas reales. Por ejemplo, la variable x da significado a la cantidad de bacterias que crecen exponencialmente en un cultivo (la cantidad de bacteria aumenta); o bien x representa la desintegración del carbono-14 en determinado periodo de tiempo (la cantidad carbono -14 disminuye).