Vuelta (ángulo)

De Wikipedia, la enciclopedia libre
Vuelta
Equivalencias
radianes 1 Vuelta = 6.283285307179586... rad
radianes 1 Vuelta = 2Π rad
Grados 1 Vuelta = 360°
Grados centesimales 1 Vuelta = 400g
[editar datos en Wikidata]
Rotaciones en sentido contrario a las agujas del reloj alrededor del punto central, donde una rotación completa es igual a 1 vuelta

Una vuelta es una unidad de medida angular igual a 2π radianes, 360 grados o 400 gonios. A su vez, también se conoce como ciclo, revolución (abreviada rev), rotación completa (abreviada rot) o círculo completo.

Subdivisiones usuales de una vuelta son la media vuelta, un cuarto de vuelta, un centésima, una milésima, o un punto del compás.

Subdivisión de una vuelta[editar]

Una vuelta se puede dividir en 100 centivueltas o en 1000 milivueltas. Cada milivuelta corresponde a un ángulo de 0,36°, que también se puede escribir como 21′ 36″. Un transportador dividido en centivueltas normalmente se llama un transportador de porcentaje.

También se utilizan fracciones binarias de una vuelta. Los marinos han dividido tradicionalmente una vuelta en 32 puntos del compás. El grado binario, también conocido como radián binario (o Brad), es 1/256 de vuelta.[1]​ El grado binario se usa en computación para que un ángulo pueda representarse con la máxima precisión posible con un solo byte. Otras medidas de ángulo utilizadas en la computación pueden basarse en dividir un giro completo en 2n partes iguales para otros valores de n.[2]​

La noción de vuelta se usa comúnmente para rotaciones planas.

Historia[editar]

La palabra vuelta procede del latín vulgar *volŭta, y este del latín volūta, participio pasado de volvĕre 'hacer rodar, voltear', 'enrollar', 'desenrollar'.[3]​

En 1697, David Gregory usó π/ρ (pi sobre rho) para denotar el perímetro de un círculo (es decir, la longitud de su circunferencia) dividida por su radio.[4]​[5]​ Sin embargo, a principios de 1647, William Oughtred había usado δ/π (delta sobre pi) para la relación del diámetro respecto al perímetro. El primer uso del símbolo π por sí mismo con su significado actual (del perímetro dividido por el diámetro) data de 1706, por el matemático galés William Jones.[6]​ Euler adoptó el símbolo con ese significado en 1737, lo que llevó a su uso generalizado.

Los transportadores de porcentaje han existido desde 1922,[7]​ pero los términos centivuelta y milivuelta fueron introducidos mucho más tarde por Fred Hoyle.[8]​

Símbolos de la unidad[editar]

La norma alemana DIN 1315 (1974-03) propuso como símbolo de la unidad la abreviatura pla (del latín: plenus angulus, "ángulo completo") para las vueltas.[9]​[10]​ Desde 2011, los lenguajes gráficos HP 39gII y HP Prime son compatibles con el símbolo de la unidad tr para vuelta. En 2016, también se agregó al código newRPL para el HP 50g.[11]​ En junio de 2017, para la versión 3.6, el lenguaje de programación Python adoptó la abreviatura tau para representar el número de radianes en una vuelta.[12]​

La norma ISO 80000-3:2006 menciona que la unidad de nombre revolución con el símbolo r se utiliza con máquinas rotativas, así como el uso del término vuelta para indicar una rotación completa. El estándar IEEE 260.1:2004 también denomina la unidad como rotación, con el símbolo r.

Conversión de unidades[editar]

La circunferencia del círculo unitario (cuyo radio es uno) mide 2π

Una vuelta es igual a 2π (≈ 6.283185307179586)[13]​ radianes.

Conversión de ángulos comunes
Vueltas Radianes Grados Gonios
0 0 0° 0g
1/24 Π/12 15° 16 2/3g
1/12 Π/6 30° 33 1/3g
1/10 Π/5 36° 40g
1/8 Π/4 45° 50g
1/2Π 1 aprox. 57.3° aprox. 63.7g
1/6 Π/3 60° 66 2/3g
1/5 2Π/5 72° 80g
1/4 Π/2 90° 100g
1/3 2Π/3 120° 133 1/3g
2/5 4Π/5 144° 160g
1/2 Π 180° 200g
3/4 3Π/2 270° 300g
1 2Π 360° 400g

Propuesta tau[editar]

Artículo principal: Tau (2π)
Un arco de círculo con la misma longitud que el radio de ese círculo corresponde a un ángulo de 1 radián. Un círculo completo corresponde a un giro completo, o aproximadamente 6.28 radianes, que se expresa aquí usando la letra griega tau (τ)

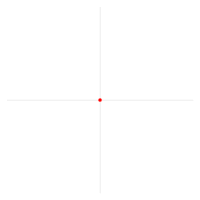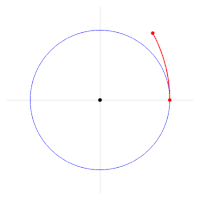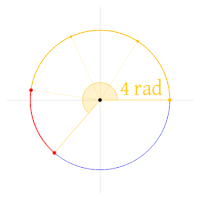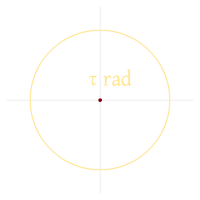
En 2001, Bob Palais propuso usar el número de radianes en una vuelta como constante fundamental del círculo (en lugar de π, que equivale al número de radianes de media vuelta), para hacer que las matemáticas sean más sencillas e intuitivas. Su propuesta utilizó un símbolo de "pi con tres patas" para denotar la constante ( = 2 π).[14]​

En 2010, Michael Hartl propuso usar tau para representar la constante del círculo de Palais: τ = 2π . Argumentó dos razones:

  • Primero, τ es el número de radianes en una vuelta, que permitiría expresar las fracciones de una vuelta más directamente: por ejemplo, 3/4  de vuelta estaría representado como 3/4τ  rad, en lugar de 3/2π  rad.
  • Segundo, τ se asemeja visualmente a π, cuya asociación con la constante del círculo es inevitable.[15]​

En su Manifiesto de Tau, Hartl[16]​ da muchos ejemplos de fórmulas que se afirma que son más claras cuando se usa tau en lugar de pi.[17]​[18]​[19]​

La constante τ está disponible en la calculadora de Google y en varios lenguajes de programación como Python,[20]​ Perl,[21]​ Processing,[22]​ y Nim.[23]​ También se ha utilizado en al menos un artículo de investigación matemática,[24]​ escrito por el promotor de τ P. Harremoës.[25]​

Sin embargo, ninguna de estas propuestas ha recibido una aceptación generalizada por parte de las comunidades matemática y científica.[26]​

Ejemplos de uso[editar]

  • Como una unidad angular, la vuelta o revolución es particularmente útil para ángulos grandes, como los utilizados para caracterizar las bobinas electromagnéticas y los objetos giratorios (véase también el número de arrollamiento).
  • La velocidad angular de la maquinaria rotativa, como los motores de los automóviles, se mide comúnmente en revoluciones por minuto o RPM.
  • La vuelta se utiliza en dinámicas complejas para medir ángulos externos e internos. La suma de los ángulos externos de un polígono es igual a una vuelta. Se utiliza la transformación diádica.
  • Los gráficos circulares ilustran proporciones de un entero como fracciones de una vuelta. Cada porcentaje se muestra como la medida correspondiente de un ángulo en centivueltas.

Cinemática de las vueltas[editar]

En cinemática, un giro es una rotación menor que una revolución completa. Un giro se puede representar en un modelo matemático que utiliza expresiones de números complejos o cuaterniones. En el plano complejo, cada número que no sea cero tiene una expresión en coordenadas polares z = r cis(a) = r cos(a) + ri sin(a) donde r > 0 y a está en [0, 2 pi). Un giro en el plano complejo se obtiene al multiplicar z = x + iy por un elemento u = exp(b i) que se encuentra en el círculo unitario:

z ↦ uz .

Frank Morley se refería constantemente a los elementos del círculo unitario como giros en el libro Geometría inversa, (1933), del que fue coautor con su hijo Frank Vigor Morley.[27]​

El término latino para vuelta es versor, que es un cuaternión que puede visualizarse como un arco de un círculo máximo. El producto de dos versores puede compararse con un triángulo esférico, donde dos lados se suman al tercero. La cinemática de la rotación en tres dimensiones, se detalla en el artículo dedicado a los cuaterniones y a la rotación espacial. Esta expresión algebraica de la rotación fue iniciada por W. R. Hamilton en la década de 1840 (usando el término versor), y es un tema recurrente en las obras de N. Mukunda como "la teoría de los giros de Hamilton".

Véase también[editar]

Referencias[editar]

  1. ↑ «ooPIC Programmer's Guide». www.oopic.com. Archivado desde el original el 28 de junio de 2008. 
  2. ↑ Hargreaves, Shawn. «Angles, integers, and modulo arithmetic». blogs.msdn.com. 
  3. ↑ Real Academia Española. «Vuelta». Diccionario de la lengua española (23.ª edición). 
  4. ↑ Beckmann, Petr (1989). A History of Pi. Barnes & Noble Publishing. 
  5. ↑ Schwartzman, Steven (1994). The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English. The Mathematical Association of America. p. 165. 
  6. ↑ «Pi through the ages». Archivado desde el original el 6 de marzo de 2012. Consultado el 22 de julio de 2019. 
  7. ↑ «A Percentage Protractor». Journal of the American Statistical Association 18: 108-109. 1922. doi:10.1080/01621459.1922.10502455. 
  8. ↑ Hoyle, Fred (1962). Astronomy. London: Macdonald. 
  9. ↑ German, Sigmar; Drath, Peter (13 de marzo de 2013). Handbuch SI-Einheiten: Definition, Realisierung, Bewahrung und Weitergabe der SI-Einheiten, Grundlagen der Präzisionsmeßtechnik (en alemán) (1 edición). Friedrich Vieweg & Sohn Verlagsgesellschaft mbH, reprint: Springer-Verlag. ISBN 3322836061. 978-3-528-08441-7, 9783322836069. Consultado el 14 de agosto de 2015. 
  10. ↑ Kurzweil, Peter (9 de marzo de 2013). Das Vieweg Einheiten-Lexikon: Formeln und Begriffe aus Physik, Chemie und Technik (en alemán) (1 edición). Vieweg, reprint: Springer-Verlag. ISBN 3322929205. doi:10.1007/978-3-322-92920-4. 978-3-322-92921-1. Consultado el 14 de agosto de 2015. 
  11. ↑ http://www.hpmuseum.org/forum/thread-4783-post-55836.html#pid55836
  12. ↑ https://www.python.org/dev/peps/pep-0628/
  13. ↑ Sequence A019692
  14. ↑ «Pi is Wrong». The Mathematical Intelligencer (New York, USA: Springer-Verlag) 23 (3): 7-8. 2001. doi:10.1007/bf03026846. 
  15. ↑ Hartl, Michael (14 de marzo de 2013). «The Tau Manifesto». Consultado el 14 de septiembre de 2013. 
  16. ↑ https://hexnet.org/files/documents/tau-manifesto.pdf
  17. ↑ «Interview: Michael Hartl: It's time to kill off pi». New Scientist 209 (2794): 23. 8 de enero de 2011. Bibcode:2011NewSc.209...23A. doi:10.1016/S0262-4079(11)60036-5. 
  18. ↑ Landau, Elizabeth (14 de marzo de 2011). «On Pi Day, is 'pi' under attack?». cnn.com. 
  19. ↑ «Why Tau Trumps Pi». 25 de junio de 2014. Consultado el 20 de marzo de 2015. 
  20. ↑ «Python 3.7.0 documentation». 
  21. ↑ «Perl 6». 
  22. ↑ «Processing». 
  23. ↑ «Nim». 
  24. ↑ Harremoës, Peter. «Bounds on tail probabilities for negative binomial distributions». Kybernetika 52 (6): 943-966. doi:10.14736/kyb-2016-6-0943. 
  25. ↑ Harremoës, Peter. «Al-Kashi's constant τ». Consultado el 20 de septiembre de 2018. 
  26. ↑ «Life of pi in no danger – Experts cold-shoulder campaign to replace with tau». Telegraph India. 30 de junio de 2011. Archivado desde el original el 13 de julio de 2013. 
  27. ↑ Morley, Frank; Morley, Frank Vigor (2014). Inversive Geometry. Boston, USA; New York, USA: Ginn and Company, reprint: Courier Corporation, Dover Publications. ISBN 978-0-486-49339-8. 0-486-49339-3. Consultado el 17 de octubre de 2015. 

Enlaces externos[editar]

Obtenido de «https://es.wikipedia.org/w/index.php?title=Vuelta_(ángulo)&oldid=159548262»